题目内容
已知函数f（x）=x2+mx+2在（-∞，1）上是减函数，在（1，+∞）上是增函数，求实数m的值，并根据所求的m的值求函数在（-∞，+∞）上的最值．
考点：二次函数的性质,函数的最值及其几何意义
专题：函数的性质及应用
分析：由函数f（x）=x2+mx+2在（-∞，1）上是减函数，在（1，+∞）上是增函数，可得：函数f（x）=x2+mx+2的图象关于直线x=1对称，进而根据二次函数的图象和性质，可得函数f（x）的最小值为1．
解答：
解：函数f（x）=x2+mx+2在（-∞，1）上是减函数，在（1，+∞）上是增函数，
故函数f（x）=x2+mx+2的图象关于直线x=1对称，
即-
=1，
解得m=-2，
故f（x）=x2-2x+2=（x-1）2+1，
故当x=1时，函数f（x）取最小值1．
故函数f（x）=x2+mx+2的图象关于直线x=1对称，
即-
| m |
| 2 |
解得m=-2，
故f（x）=x2-2x+2=（x-1）2+1，
故当x=1时，函数f（x）取最小值1．
点评：本题考查的知识点是二次函数的性质，函数的最值及其几何意义，熟练掌握二次函数的图象和性质是解答的关键．
练习册系列答案
相关题目
如图，在四棱锥P-ABCD中，侧面PAD是正三角形，且与底面ABCD垂直，底面ABCD是边长为2的菱形，∠BAD=60°，N是PB的中点，过A、D、N三点的平面交PC于M，E为AD的中点，求证：已知在某班有
的学生数学成绩优秀，如果从班中随机地找出5名学生，那么其中数学成绩优秀的学生X～B（5，
），则E（-X）的值为（ ）
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
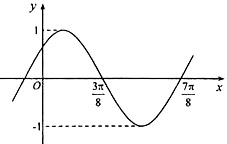已知函数y=sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、y=sin（2x+
| ||
B、y=sin（2x+
| ||
C、y=sin（4x+
| ||
D、y=sin（4x+
|