题目内容
已知f（3x+1）=9x2-6x+5，求函数f（x）的解析式．
考点：函数解析式的求解及常用方法
专题：换元法
分析：先令3x+1=t求出x的值，然后代入函数表达式整理即可．
解答：
解：令3x+1=t，则x=
，
∴f（t）=9•(
)2-6•
+5，
整理得：f（t）=t2-4t+8，
∴f（x）=x2-4x+8．
| t-1 |
| 3 |
∴f（t）=9•(
| t-1 |
| 3 |
| t-1 |
| 3 |
整理得：f（t）=t2-4t+8，
∴f（x）=x2-4x+8．
点评：本题考察了函数解析式的求解，求函数解析式方法多种，在复习时可进行整理．
练习册系列答案
相关题目
曲线C1：y=
ex关于直线y=x对称得曲线C2，动点P在C1上，动点Q在C2上，则|PQ|最小值为（ ）
| 1 |
| 2 |
| A、1-ln2 | ||
B、
| ||
| C、1+ln2 | ||
D、
|
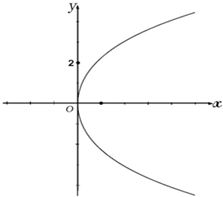已知曲线Γ：y2=4x，直线l经过点（0，2）且其一个方向向量为