题目内容
在△ABC中,角A,B,C所对应的边分别为a,b,c,tan
+tan
=4,2sinBcosC=sinA.
(1)求角A的大小;
(2)若S△ABC=
,求边a的大小.
| A+B |
| 2 |
| C |
| 2 |
(1)求角A的大小;
(2)若S△ABC=
| 3 |
考点:正弦定理,三角函数中的恒等变换应用
专题:解三角形
分析:(1)把tan
+tan
=4转化成正弦和余弦的关系式,求得sinC的值,进而求得C,整理2sinBcosC=sinA可求得sin(B-C)=0,判断出B=C,进而求得A.
(2)利用正弦定理求得b的表达式,代入三角形面积公式求得答案.
| A+B |
| 2 |
| C |
| 2 |
(2)利用正弦定理求得b的表达式,代入三角形面积公式求得答案.
解答:
解:∵tan
+tan
=4,
∴
+
=4,
∴
=4,
∴sinC=
,
∵C∈(0,π),
∴C=
或
∵2sinBcosC=sinA
∴2sinBcosC=sin(B+C)=sinBcosC+cosBsinC,
∴sinBcosC-cosBsinC=0,即sin(B-C)=0,
∴C=B=
,
∵A=π-C-B=
,.
(2)∵
=
,
∴b=
•sinB=
a,
∵C=B
∴c=b
∴S△ABC=
bcsinA=
×
a×
a×
=
a2=
,
∴a=2
.
| A+B |
| 2 |
| C |
| 2 |
∴
cos
| ||
sin
|
sin
| ||
cos
|
∴
| 1 | ||||
sin
|
∴sinC=
| 1 |
| 2 |
∵C∈(0,π),
∴C=
| π |
| 6 |
| 5π |
| 6 |
∵2sinBcosC=sinA
∴2sinBcosC=sin(B+C)=sinBcosC+cosBsinC,
∴sinBcosC-cosBsinC=0,即sin(B-C)=0,
∴C=B=
| π |
| 6 |
∵A=π-C-B=
| 2π |
| 3 |
(2)∵
| a |
| sinA |
| b |
| sinB |
∴b=
| a |
| sinA |
| ||
| 3 |
∵C=B
∴c=b
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
| ||
| 12 |
| 3 |
∴a=2
| 3 |
点评:本题主要考查了正弦定理的运用,三角形恒等变换的应用.要充分利用好已知条件,必须是先化简再求值.

练习册系列答案
相关题目
已知向量
=(2,-3,5)与向量
=(3,λ,
)平行,则λ=( )
| a |
| b |
| 15 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
若P是抛物线x2=4y上的一个动点,则点P到直线l1:y=-1,l2:3x+4y+12=0的距离之和的最小值为( )
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
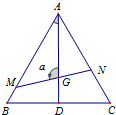 如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[
如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[