题目内容
已知曲线f(x)=
x3+3x+
,求与直线4x-y-2=0平行的该曲线的切线方程.
| 1 |
| 3 |
| 2 |
| 3 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:设出切点坐标,求出原函数的导函数,得到函数在切点处的导数值,由导数值等于4求得切点横坐标,进一步求出切点坐标,代入直线方程的点斜式求得切线方程.
解答:
解:由f(x)=
x3+3x+
,得f′(x)=x2+3,
设与直线4x-y-2=0平行的该曲线的切线的切点为(x0,y0),
则f′(x0)=x02+3.
由x02+3=4,得x0=±1.
当x0=1时,y0=
×13+3×1+
=4.
切线方程为y-4=4×(x-1),即4x-y=0;
当x0=-1时,y0=
×(-1)3+3×(-1)+
=-
.
切线方程为y+
=4×(x+1),即12x-3y+4=0.
∴与直线4x-y-2=0平行的曲线的切线方程为4x-y=0,12x-3y+4=0.
| 1 |
| 3 |
| 2 |
| 3 |
设与直线4x-y-2=0平行的该曲线的切线的切点为(x0,y0),
则f′(x0)=x02+3.
由x02+3=4,得x0=±1.
当x0=1时,y0=
| 1 |
| 3 |
| 2 |
| 3 |
切线方程为y-4=4×(x-1),即4x-y=0;
当x0=-1时,y0=
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
切线方程为y+
| 8 |
| 3 |
∴与直线4x-y-2=0平行的曲线的切线方程为4x-y=0,12x-3y+4=0.
点评:本题考查利用导数研究曲线上某点处的切线方程,函数在某点处的导数,就是曲线过该点的切线的斜率,是中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知复数z满足z•(1-i)=3+i,i为虚数单位,则|z|=( )
A、
| ||
B、
| ||
| C、5 | ||
| D、3 |
已知曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,设函数f(x)=g(2x-1),则曲线y=f(x)在点(1,f(1))处切线方程为( )
| A、y=2x+1 |
| B、y=4x-1 |
| C、y=2x-1 |
| D、y=4x+1 |
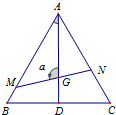 如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[
如图,△ABC是边长为1的正三角形,M,N分别是边AB,AC上的点,线段MN过△ABC的重心G,设∠MGA=α,α∈[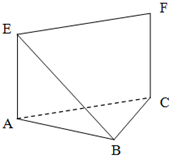 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.