题目内容
已知a,b∈N,a≠b,且a2-b2=a3-b3,比较a+b,1,
大小.
| 4 |
| 3 |
考点:不等式比较大小
专题:不等式的解法及应用
分析:根据条件进行化简,利用基本不等式即可比较大小.
解答:
解:由a2-b2=a3-b3,得(a-b)(a+b)=(a-b)(a2+ab+b2),
∵a≠b,
∴a+b=a2+ab+b2,
即(a+b)2-(a+b)=ab,
∵0<ab<
,
∴(a+b)2-(a+b)=ab<
,
∵a,b∈N,a≠b,
∴a+b≥1,
即a+b-1<
(a+b),
即a+b<
,
综上得1≤a+b<
.
∵a≠b,
∴a+b=a2+ab+b2,
即(a+b)2-(a+b)=ab,
∵0<ab<
| (a+b)2 |
| 4 |
∴(a+b)2-(a+b)=ab<
| (a+b)2 |
| 4 |
∵a,b∈N,a≠b,
∴a+b≥1,
即a+b-1<
| 1 |
| 4 |
即a+b<
| 4 |
| 3 |
综上得1≤a+b<
| 4 |
| 3 |
点评:本题主要考查不等式的大小比较,利用基本不等式是解决本题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
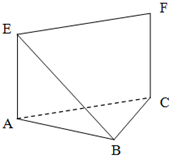 如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.
如图,等腰直角△ABC中,∠ABC=90°,EA⊥平面ABC,FC∥EA,EA=FC=AB=a.