题目内容
已知函数f(x)与g(x)的公共定义域为I,函数h(x)满足:对任意x∈I,点(x,h(x))与点(x,g(x))均关于点(x,f(x))对称,若f(x)=alnx-x2+ax(a>0),对任意x∈R,函数g(x)满足2g(x)-g(1-x)=2ex-
+1,其中e=2.71828…为自然对数的底数,有下列命题:
①当a=1时,曲线y=h(x)在x=1处的切线的斜率为-e-2;
②当a=1,x∈[1,+∞)时,函数h(x)的值域为(-∞,-e-1];
③若函数f(x)在(0,2)内不单调,则a的取值范围为(0,2);
④设函数F(x)=bln[g(x)-1]+f′(x)+2x-a,其中b>0,f′(x)为f(x)的导函数,若O为坐标原点,函数F(x)的图象为C,则对任意点M∈C,都存在唯一点N∈C,使得tan∠MON=b.
其中真命题的个数为( )
| 1 |
| ex-1 |
①当a=1时,曲线y=h(x)在x=1处的切线的斜率为-e-2;
②当a=1,x∈[1,+∞)时,函数h(x)的值域为(-∞,-e-1];
③若函数f(x)在(0,2)内不单调,则a的取值范围为(0,2);
④设函数F(x)=bln[g(x)-1]+f′(x)+2x-a,其中b>0,f′(x)为f(x)的导函数,若O为坐标原点,函数F(x)的图象为C,则对任意点M∈C,都存在唯一点N∈C,使得tan∠MON=b.
其中真命题的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:利用导数研究曲线上某点切线方程
专题:阅读型,函数的性质及应用,导数的概念及应用,导数的综合应用
分析:运用中点坐标公式可得2f(x)=g(x)+h(x),再由x换为1-x,运用函数方程的思想可得g(x),h(x),
求出h(x)的导数,由导数的几何意义,即可得到切线的斜率,即可判断①;求出h(x)的导数,判断[1,+∞)的单调性,即可得到值域,进而判断②;若函数f(x)在(0,2)内单调,运用导数和不等式恒成立求得a的范围,再求补集,即可判断③;先化简F(x),令h(x)=bx,判断y=bx为F(x)的渐近线,检验在函数f(x)图象上任取两点M,N,∠MON<arctanb或∠MON>π-arctanb,即可判断④.
求出h(x)的导数,由导数的几何意义,即可得到切线的斜率,即可判断①;求出h(x)的导数,判断[1,+∞)的单调性,即可得到值域,进而判断②;若函数f(x)在(0,2)内单调,运用导数和不等式恒成立求得a的范围,再求补集,即可判断③;先化简F(x),令h(x)=bx,判断y=bx为F(x)的渐近线,检验在函数f(x)图象上任取两点M,N,∠MON<arctanb或∠MON>π-arctanb,即可判断④.
解答:
解:由题意可得2f(x)=g(x)+h(x),又对任意x∈R,函数g(x)满足2g(x)-g(1-x)=2ex-
+1,将x换为1-x,可得2g(1-x)-g(x)=2e1-x-ex+1,消去g(1-x),可得g(x)=ex+1,h(x)=2f(x)-g(x)=2alnx-2x2+2ax-ex-1,
对于①,当a=1时,y=h(x)=2lnx-2x2+2x-ex-1的导数为y′=
-4x+2-ex,曲线y=h(x)在x=1处的切线的斜率为2-4+2-e=-e,则①错;
对于②,当a=1,x∈[1,+∞)时,y=h(x)=2lnx-2x2+2x-ex-1的导数为y′=
-4x+2-ex<0,
函数h(x)递减,即有h(x)≤h(1)=-e-1,则②正确;
对于③,若函数f(x)在(0,2)内单调,f(x)=alnx-x2+ax(a>0)的导数为f′(x)=
-2x+a,
即有f′(x)=
,若f(x)在(0,2)内递增,即有-2x2+ax+a≥0在(0,2)恒成立,
即a≥
=2[
+(x+1)-2],由x∈(0,2),x+1∈(1,3),可得2[
+(x+1)-2]∈(0,
),
即有a≥
;若f(x)在(0,2)内递减,即有-2x2+ax+a≤0在(0,2)恒成立,
即a≤
=2[
+(x+1)-2],由x∈(0,2),x+1∈(1,3),可得2[
+(x+1)-2]∈(0,
),
即a≤0,与a>0矛盾,综上可得若函数f(x)在(0,2)内不单调,则a的取值范围为(0,
)
则③错;
对于④,函数F(x)=bln[g(x)-1]+f′(x)+2x-a=blnex+
-2x+a+2x-a=bx+
,
令h(x)=bx,则F(x)-h(x)=bx+
-bx=
,(a>0,b>0),
当x→+∞时,
→0,h(x)=bx是函数y=bx+
的渐近线,
在函数F(x)图象上任取两点M,N,∠MON<arctanb或∠MON>π-arctanb,
则tan∠MON>b或-b<tan∠MON<0,即此时不存在这样的两点M,N,使得tan∠MON=b,则④错误.
综上可得,其中真命题的个数为1.
故选:A.
| 1 |
| ex-1 |
对于①,当a=1时,y=h(x)=2lnx-2x2+2x-ex-1的导数为y′=
| 2 |
| x |
对于②,当a=1,x∈[1,+∞)时,y=h(x)=2lnx-2x2+2x-ex-1的导数为y′=
| 2 |
| x |
函数h(x)递减,即有h(x)≤h(1)=-e-1,则②正确;
对于③,若函数f(x)在(0,2)内单调,f(x)=alnx-x2+ax(a>0)的导数为f′(x)=
| a |
| x |
即有f′(x)=
| -2x2+ax+a |
| x |
即a≥
| 2x2 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x+1 |
| 8 |
| 3 |
即有a≥
| 8 |
| 3 |
即a≤
| 2x2 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x+1 |
| 8 |
| 3 |
即a≤0,与a>0矛盾,综上可得若函数f(x)在(0,2)内不单调,则a的取值范围为(0,
| 8 |
| 3 |
则③错;
对于④,函数F(x)=bln[g(x)-1]+f′(x)+2x-a=blnex+
| a |
| x |
| a |
| x |
令h(x)=bx,则F(x)-h(x)=bx+
| a |
| x |
| a |
| x |
当x→+∞时,
| a |
| x |
| a |
| x |
在函数F(x)图象上任取两点M,N,∠MON<arctanb或∠MON>π-arctanb,
则tan∠MON>b或-b<tan∠MON<0,即此时不存在这样的两点M,N,使得tan∠MON=b,则④错误.
综上可得,其中真命题的个数为1.
故选:A.
点评:本题考查导数的运用:求切线的斜率和求单调区间,主要考查函数的单调性的运用,以及分类讨论的思想方法,属于中档题和易错题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )
A、
| ||
| B、sin0.5 | ||
| C、2sin0.5 | ||
| D、tan0.5 |
若x2cosα+y2sinα+1=0(α∈(0,2π))表示一个圆,则( )
A、0<α<
| ||
B、π<α<
| ||
C、α=
| ||
D、α=
|
已知集合A={x|x2≥1},B={x|y=
},则A∩∁RB=( )
| 1-log2x |
| A、(2,+∞) |
| B、(-∞,-1]∪(2,+∞) |
| C、(-∞,-1)∪(2,+∞) |
| D、[-1,0]∪[2,+∞) |
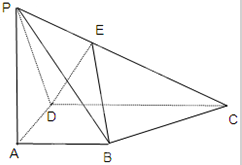 如图,PA⊥平面ABCD,底面ABCD是直角梯形,AB⊥AD,AB=AD,CD=2AB,E为PC中点.若PB与平面ABCD所成的角为45°
如图,PA⊥平面ABCD,底面ABCD是直角梯形,AB⊥AD,AB=AD,CD=2AB,E为PC中点.若PB与平面ABCD所成的角为45° 已知P是抛物线x2=2py(p>0)上的动点,P到抛物线焦点的距离比到x轴的距离大1.
已知P是抛物线x2=2py(p>0)上的动点,P到抛物线焦点的距离比到x轴的距离大1.