题目内容
 已知P是抛物线x2=2py(p>0)上的动点,P到抛物线焦点的距离比到x轴的距离大1.
已知P是抛物线x2=2py(p>0)上的动点,P到抛物线焦点的距离比到x轴的距离大1.(1)求该抛物线的方程;
(2)如图,C,D是y轴正半轴上的两个不同的点,直线PC,PD分别交抛物线于另外一点G,H,作直线GH的平行线l与抛物线相切,切点为Q,求证:△PCQ与△PDQ的面积相等.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由P到抛物线焦点的距离比到x轴的距离大1,可得
=1,解得p即可得出.
(2)设P(x1,y1),G(x2,y2),H(x3,y3),Q(s,t),kPG=k1,kPH=k2.PQ与y轴的交点为M.直线PG的方程为:y-y1=k(x-x1),y1=
.与抛物线的方程联立可得x2-4k1x+4k1x1-
=0,可得x2=4k1-x1,x3=4k2-x1.由于kGH=
.由x2=4y,利用导数可得y′|x=s=
s.因此
=
s,可得2k1+2k2-x1=s.直线PQ的方程为:y-
=
(x-x1),可得yM=-
=-
(2k1+2k2-x1).分别求出直线PG,PH与y轴的交点,只要证明
=yM即可证明.
| p |
| 2 |
(2)设P(x1,y1),G(x2,y2),H(x3,y3),Q(s,t),kPG=k1,kPH=k2.PQ与y轴的交点为M.直线PG的方程为:y-y1=k(x-x1),y1=
| ||
| 4 |
| x | 2 1 |
| x3+x2 |
| 4 |
| 1 |
| 2 |
| x2+x3 |
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| s+x1 |
| 4 |
| sx1 |
| 4 |
| x1 |
| 4 |
| yC+yD |
| 2 |
解答:
解:(1)∵P到抛物线焦点的距离比到x轴的距离大1,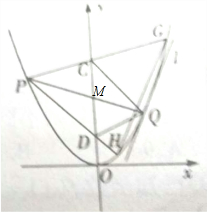
∴
=1,解得p=2.
∴该抛物线的方程为x2=4y;
(2)设P(x1,y1),G(x2,y2),H(x3,y3),Q(s,t),kPG=k1,kPH=k2.PQ与y轴的交点为M.
直线PG的方程为:y-y1=k(x-x1),y1=
.
联立
,化为x2-4k1x+4k1x1-
=0,
∴x1+x2=4k1,
∴x2=4k1-x1.
同理可得:x3=4k2-x1.
kGH=
=
=
.
由x2=4y,可得y′=
x,
∴y′|x=s=
s.
由题意可得:
=
s,
∴x2+x3=2s.
∴4k1+4k2-2x1=2s,
∴2k1+2k2-x1=s.
直线PQ的方程为:y-
=
(x-x1),
化为y-
=
(x-x1),
令x=0,解得yM=-
=-
(2k1+2k2-x1).
由直线PG的方程:y-
=k1(x-x1),
令x=0,可得yC=
-k1x1,
同理可得yD=
-k1x1.
∴
=-
(2k1+2k2-x1).
∴直线PQ与y轴的交点M为线段CD的中点,
∴△PCQ与△PDQ的面积相等.

∴
| p |
| 2 |
∴该抛物线的方程为x2=4y;
(2)设P(x1,y1),G(x2,y2),H(x3,y3),Q(s,t),kPG=k1,kPH=k2.PQ与y轴的交点为M.
直线PG的方程为:y-y1=k(x-x1),y1=
| ||
| 4 |
联立
|
| x | 2 1 |
∴x1+x2=4k1,
∴x2=4k1-x1.
同理可得:x3=4k2-x1.
kGH=
| y3-y2 |
| x3-x2 |
| ||||||||
| x3-x2 |
| x3+x2 |
| 4 |
由x2=4y,可得y′=
| 1 |
| 2 |
∴y′|x=s=
| 1 |
| 2 |
由题意可得:
| x2+x3 |
| 4 |
| 1 |
| 2 |
∴x2+x3=2s.
∴4k1+4k2-2x1=2s,
∴2k1+2k2-x1=s.
直线PQ的方程为:y-
| ||
| 4 |
| ||||||
| s-x1 |
化为y-
| ||
| 4 |
| s+x1 |
| 4 |
令x=0,解得yM=-
| sx1 |
| 4 |
| x1 |
| 4 |
由直线PG的方程:y-
| ||
| 4 |
令x=0,可得yC=
| ||
| 4 |
同理可得yD=
| ||
| 4 |
∴
| yC+yD |
| 2 |
| x1 |
| 4 |
∴直线PQ与y轴的交点M为线段CD的中点,
∴△PCQ与△PDQ的面积相等.
点评:本题考查了抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立得出根与系数的关系、中点坐标公式、三角形的面积之比、斜率计算公式、利用导数研究切线的斜率,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
下列函数中在区间[1,2]上有零点的是( )
| A、f(x)=3x2-4x+5 |
| B、f(x)=x2-5x-5 |
| C、f(x)=lnx-3x+6 |
| D、f(x)=ex+3x-6 |