题目内容
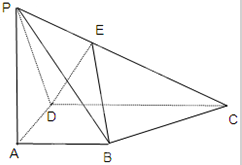 如图,PA⊥平面ABCD,底面ABCD是直角梯形,AB⊥AD,AB=AD,CD=2AB,E为PC中点.若PB与平面ABCD所成的角为45°
如图,PA⊥平面ABCD,底面ABCD是直角梯形,AB⊥AD,AB=AD,CD=2AB,E为PC中点.若PB与平面ABCD所成的角为45°(1)求异面直线PD与BE所成角的大小;
(2)求二面角E-BD-C的大小.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:空间角
分析:(1)以A为原点,AB为x轴,AD为y轴,建立空间直角坐标系,设异面直线PD与BE所成角为θ,由cosθ=|cos<
,
>|=
,利用向量法能求出异面直线PD与BE所成角.
(2)求出平面BDE的法向量和平面BDC的法向量,利用向量法能求出二面角E-BD-C的大小.
| PD |
| BE |
|
| ||||
|
|
(2)求出平面BDE的法向量和平面BDC的法向量,利用向量法能求出二面角E-BD-C的大小.
解答:
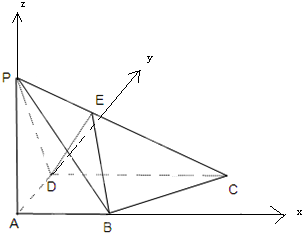 解:(1)以A为原点,AB为x轴,AD为y轴,
解:(1)以A为原点,AB为x轴,AD为y轴,
建立空间直角坐标系,
设AB=AD=1,则CD=2,AP=AB=1,
P(0,0,1),D(0,1,0),C(2,1,0),
B(1,0,0),E(1,
,
),
=(0,1,-1),
=(0,
,
),
设异面直线PD与BE所成角为θ,
cosθ=|cos<
,
>|=
=
=0,
∴异面直线PD与BE所成角为90°.
(2)
=(1,0,0),
=(1,
,
),
设平面BDE的法向量
=(x,y,z),
则
,
取y=1,得
=(0,1,-1),
又平面BDC的法向量
=(0,0,1),
设二面角E-BD-C的大小为θ,
cosθ=
=
=
.
∴θ=45°.
∴二面角E-BD-C的大小为45°.
 解:(1)以A为原点,AB为x轴,AD为y轴,
解:(1)以A为原点,AB为x轴,AD为y轴,建立空间直角坐标系,
设AB=AD=1,则CD=2,AP=AB=1,
P(0,0,1),D(0,1,0),C(2,1,0),
B(1,0,0),E(1,
| 1 |
| 2 |
| 1 |
| 2 |
| PD |
| BE |
| 1 |
| 2 |
| 1 |
| 2 |
设异面直线PD与BE所成角为θ,
cosθ=|cos<
| PD |
| BE |
|
| ||||
|
|
=
| ||||||
|
∴异面直线PD与BE所成角为90°.
(2)
| DB |
| DE |
| 1 |
| 2 |
| 1 |
| 2 |
设平面BDE的法向量
| n |
则
|
取y=1,得
| n |
又平面BDC的法向量
| m |
设二面角E-BD-C的大小为θ,
cosθ=
|
| ||||
|
|
| 1 | ||
|
| ||
| 2 |
∴θ=45°.
∴二面角E-BD-C的大小为45°.
点评:本题考查异面直线PD与BE所成角的大小的求法,考查二面角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知函数f(x)=
,若函数g(x)=f(x)-m有三个零点,则实数m的取值范围是( )
|
A、(0,
| ||
B、(
| ||
| C、(0,1) | ||
| D、(0,1] |