题目内容
15.若函数f(x)=lg(mx+$\sqrt{{x}^{2}+1}$)为奇函数,则m=( )| A. | -1 | B. | 1 | C. | -1或1 | D. | 0 |
分析 根据函数奇偶性的定义建立方程关系进行求解即可.
解答 解:∵函数f(x)=lg(mx+$\sqrt{{x}^{2}+1}$)为奇函数,
∴f(-x)=-f(x),
即lg(-mx+$\sqrt{{x}^{2}+1}$)=-lg(mx+$\sqrt{{x}^{2}+1}$),
即lg(-mx+$\sqrt{{x}^{2}+1}$)+lg(mx+$\sqrt{{x}^{2}+1}$)=0,
即lg(-mx+$\sqrt{{x}^{2}+1}$)(mx+$\sqrt{{x}^{2}+1}$)=lg(x2+1-m2x2)=0,
即x2+1-m2x2=1,
则(1-m2)x2=0,
则1-m2=0,则m=1或-1,
故选:C.
点评 本题主要考查函数奇偶性的应用,根据定义建立方程关系,结合对数的运算法则是解决本题的关键.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
6.化简:$\overrightarrow{AB}$+$\overrightarrow{OA}$-$\overrightarrow{OB}$=( )
| A. | $\overrightarrow{0}$ | B. | $\overrightarrow{BA}$ | C. | 2$\overrightarrow{AB}$ | D. | -2$\overrightarrow{AB}$ |
7.下列关于函数f(x)=sinx(cosx+sinx)的说法中,不正确的是( )
| A. | f(x)的最小正周期为π | |
| B. | f(x)的图象关于直线x=-$\frac{π}{8}$对称 | |
| C. | f(x)的图象关于点($\frac{π}{8}$,0)对称 | |
| D. | f(x)的图象向右平移$\frac{π}{8}$后得到一个偶函数的图象 |
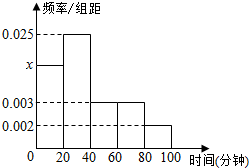 某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动
某中学随机抽取50名高一学生调查其每天运动的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,运动