题目内容
5.已知函数$f(x)={log_9}({9^x}+1)+kx(k∈R)$是偶函数.(1)求k的值;
(2)若函数y=f(x)的图象与直线$y=\frac{1}{2}x+b$没有交点,求b的取值范围.
(3)设$h(x)={log_9}(a•{3^x}-\frac{4}{3}a)$,若函数f(x)与h(x)的图象有且只有一个公共点,求实数a的取值范围.
分析 (1)根据函数的奇偶性求出k的值即可;
(2)问题转化为g(x)=log9(9x+1)-x的图象和直线y=b无交点,求出g(x)的最小值,从而求出b的范围;
(3)问题转化为方程3x+$\frac{1}{{3}^{x}}$-$\frac{4}{3}$a有且只有一个实数根,通过换元结合二次函数的性质求出a的范围即可.
解答 解:(1)因为y=f(x)为偶函数,所以?x∈R,f(-x)=f(x),
即log9(9-x+1)-kx=log9(9x+1)+kx对于?x∈R恒成立.
即2kx=${log}_{9}^{{(9}^{-x}+1)}$-${log}_{9}^{{(9}^{x}+1)}$=${log}_{9}^{\frac{{9}^{x}+1}{{9}^{x}}}$-${log}_{9}^{{(9}^{x}+1)}$=-x恒成立
即(2k+1)x=0恒成立,而x不恒为零,所以k=-$\frac{1}{2}$.
(2)由题意知方程${log}_{9}^{{(9}^{x}+1)}$-$\frac{1}{2}$x=$\frac{1}{2}$x+b即方程log9(9x+1)-x=b无解.
令g(x)=log9(9x+1)-x,则函数y=g(x)的图象与直线y=b无交点.
因为g(x)=${log}_{9}^{\frac{{9}^{x}+1}{{9}^{x}}}$=${log}_{9}^{(1+\frac{1}{{9}^{x}})}$,
任取x1、x2∈R,且x1<x2,则0<${9}^{{x}_{1}}$<${9}^{{x}_{2}}$,从而$\frac{1}{{9}^{{x}_{1}}}$>$\frac{1}{{9}^{{x}_{2}}}$.
于是${log}_{9}^{(1+\frac{1}{{9}^{{x}_{1}}})}$>${log}_{9}^{(1+\frac{1}{{9}^{{x}_{2}}})}$,即g(x1)>g(x2),
所以g(x)在(-∞,+∞)是单调减函数.
因为1+$\frac{1}{{9}^{x}}$>1,所以g(x)=${log}_{9}^{(1+\frac{1}{{9}^{x}})}$>0.
所以b的取值范围是(-∞,0].
(3)由题意知方程3x+$\frac{1}{{3}^{x}}$-$\frac{4}{3}$a有且只有一个实数根.
令3x=t>0,则关于t的方程(a-1)t2-$\frac{4}{3}$at-1=0(记为(*))
有且只有一个正根.
若a=1,则t=-$\frac{3}{4}$,不合,舍去;若a≠1,则方程(*)的两根异号或有两相等正根.
由△=0⇒a=$\frac{3}{4}$或-3;但a=$\frac{3}{4}$⇒t=-$\frac{1}{2}$,不合,舍去;而a=-3⇒t=$\frac{1}{2}$;
方程(*)的两根异号?(a-1)•(-1)<0,即-a+1<0,解得:a>1.
综上所述,实数a的取值范围{-3}∪(1,+∞).
点评 本题考查了函数的奇偶性问题,考查函数的单调性以及最值问题,考查转化思想,是一道中档题.

 为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:
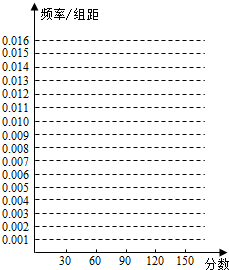
为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表:(1)求出表中m、n、M、N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图:
| 分组 | 频数 | 频率 |
| [0,30) | 3 | 0.03 |
| [30,60) | 3 | 0.03 |
| [60,90) | 37 | 0.37 |
| [90,120) | m | n |
| [120,150) | 15 | 0.15 |
| 合计 | M | N |
(3)为了深入分析学生的成绩,有关部门拟从分数不超过60的学生中选取2人进行进一步分析,求被选中2人分数均不超过30分的概率.
| A. | -1 | B. | 1 | C. | -1或1 | D. | 0 |
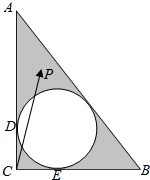 在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )
在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )