题目内容
5.已知数列{an}是等差数列,且a1=3,a1+a2+a3=15.(1)求数列{an}的通项公式;
(2)求数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和.
分析 (1)先求得a1,a2得出d,即可写出an.
(2)利用(1)可得,利用裂项相消法即可求得数列的和.
解答 解:(1)∵数列{an}是等差数列,且a1=3,a1+a2+a3=15.a2=5,
∴d=2,
∴an=3+2(n-1)=2n+1.
(2)$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$,
∴数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和Tn=$\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+$$\frac{1}{2n+1}$-$\frac{1}{2n+3}$=$\frac{1}{3}-\frac{1}{2n+3}$.
点评 本题主要考查等差数列的定义及性质和数列求和的方法裂项相消法,考查学生的运算求解能力,属中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
15.若函数f(x)=lg(mx+$\sqrt{{x}^{2}+1}$)为奇函数,则m=( )
| A. | -1 | B. | 1 | C. | -1或1 | D. | 0 |
16.已知点A(2,0),B(0,3),则直线AB的方程为( )
| A. | 3x-2y-6=0 | B. | 2x-3y+6=0 | C. | 3x+2y-6=0 | D. | 2x+3y+6=0 |
17.在下列向量组中,可以用它们作基底把向量$\overrightarrow{m}$=(-3,5)表示出来的是( )
| A. | $\overrightarrow{{e}_{1}}$=(-2,3),$\overrightarrow{{e}_{2}}$=(4,-6) | B. | $\overrightarrow{{e}_{1}}$=(1,5),$\overrightarrow{{e}_{2}}$=(-2,1) | ||
| C. | $\overrightarrow{{e}_{1}}$=(2,3),$\overrightarrow{{e}_{2}}$=(-1,-$\frac{3}{2}$) | D. | $\overrightarrow{{e}_{1}}$=(3,4),$\overrightarrow{{e}_{2}}$=(-6,-8) |
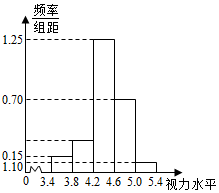 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.