题目内容
已知0＜x＜0.5，则x取何值时，x（1-2x）的值最大．
考点：函数的最值及其几何意义
专题：函数的性质及应用
分析：先研究函数y=x（1-2x）（0＜x＜
）的单调性，再求最大值．
| 1 |
| 2 |
解答：
解：令y=x（1-2x）=-2x2+x=-2（x-
）2+
，
该函数图象开口向下，对称轴x=
，所以该函数在
（0，
）上递增，在（
，
）上递减，
故ymax=f(
)=
．
| 1 |
| 4 |
| 1 |
| 8 |
该函数图象开口向下，对称轴x=
| 1 |
| 4 |
（0，
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
故ymax=f(
| 1 |
| 4 |
| 1 |
| 8 |
点评：本题考查了利用二次函数的单调性求其最值的问题，属于基础题．
练习册系列答案
相关题目
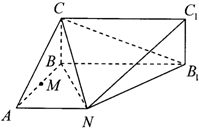已知矩形BCC1B1所在平面与平面ABB1N垂直，AN∥BB1，AB⊥BB1，且BB1=8，AN=AB=BC=4，若数列{an}的通项公式是an=（-1）n（3n-2），则a1+a2+…+a100=（ ）
| A、150 | B、120 |
| C、-120 | D、-150 |