题目内容
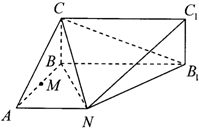已知矩形BCC1B1所在平面与平面ABB1N垂直，AN∥BB1，AB⊥BB1，且BB1=8，AN=AB=BC=4，（1）求证：BN⊥平面C1B1N；
（2）设θ为直线C1N与平面CNB1所成的角，求sinθ；
（3）设M为AB中点，在BC边上求一点P，使MP∥平面CNB1，求
| BP |
| PC |
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：综合题,空间位置关系与距离
分析：（1）BA，BC，BB1两两垂直． 以B为坐标原点，分别以BA，BC，BB1所在直线别为x，y，z轴建立空间直角坐标系，证出
•
=0，
•
=0后即可证明BN⊥平面C1B1N；
（2）求出平面NCB1的一个法向量
，利用
与此法向量的夹角求出直线C1N与平面CNB1所成的角
（3）设P（0，0，a）为BC上一点，由MP∥平面CNB1，得知
•
=0，利用向量数量积为0求出a的值，并求出
的值．
| BN |
| NB1 |
| BN |
| B1C1 |
（2）求出平面NCB1的一个法向量
| n |
| C1N |
（3）设P（0，0，a）为BC上一点，由MP∥平面CNB1，得知
| MP |
| n |
| BP |
| PC |
解答：
（1）证明：∵BA，BC，BB1两两垂直． …（2分）
以B为坐标原点，分别以BA，BC，BB1所在直线别为x，y，z轴建立空间直角坐标系，
则N（4，4，0），B1（0，8，0），C1（0，8，4），C（0，0，4）
∵
•
=（4，4，0）•（-4，4，0）=-16+16=0
•
=（4，4，0）•（0，0，4）=0
∴BN⊥NB1，BN⊥B1C1且NB1与B1C1相交于B1，
∴BN⊥平面C1B1N； …（4分）
（2）解：设
=（x，y，z）为平面NCB1的一个法向量，
则
，取
=（1，1，2），
∵
=（4，-4，-4），
∴sinθ=
；…（8分）
（3）解：∵M（2，0，0）．设P（0，0，a）为BC上一点，则
=（-2，0，a），
∵MP∥平面CNB1，
∴
•
=0
∴（-2，0，a）•（1，1，2）=0，
∴a=1．
又PM?平面CNB1，∴MP∥平面CNB1，
∴当PB=1时，MP∥平面CNB1
∴
=
…（12分）
以B为坐标原点，分别以BA，BC，BB1所在直线别为x，y，z轴建立空间直角坐标系，
则N（4，4，0），B1（0，8，0），C1（0，8，4），C（0，0，4）
∵
| BN |
| NB1 |
| BN |
| B1C1 |
∴BN⊥NB1，BN⊥B1C1且NB1与B1C1相交于B1，
∴BN⊥平面C1B1N； …（4分）
（2）解：设
| n |
则
|
| n |
∵
| C1N |
∴sinθ=
| ||
| 3 |
（3）解：∵M（2，0，0）．设P（0，0，a）为BC上一点，则
| MP |
∵MP∥平面CNB1，
∴
| MP |
| n |
∴（-2，0，a）•（1，1，2）=0，
∴a=1．
又PM?平面CNB1，∴MP∥平面CNB1，
∴当PB=1时，MP∥平面CNB1
∴
| BP |
| PC |
| 1 |
| 3 |
点评：本题主要考查了直线与平面之间的位置关系及判断，线面角求解，利用空间向量的方法，能够降低思维难度，但要注意有关的运算要准确．
练习册系列答案
相关题目