题目内容
若数列{an}的通项公式是an=（-1）n（3n-2），则a1+a2+…+a100=（ ）
| A、150 | B、120 |
| C、-120 | D、-150 |
考点：数列的求和
专题：
分析：依题意，可知a1+a2+…+a100=（a1+a2）+（a3+a4）+…+（a99+a100）=（-1+4）+（-7+10）+（-13+16）+…+（-295+298），利用等差数列的性质可得答案．
解答：
解：原式=-1+4-7+10-…-295+298
=（-1+4）+（-7+10）+（-13+16）+…+（-295+298）
=3×50=150．
故选：A．
=（-1+4）+（-7+10）+（-13+16）+…+（-295+298）
=3×50=150．
故选：A．
点评：本题考查数列的求和，分组求和是关键，考查等价转化思想与运算求解能力，属于中档题．
练习册系列答案
相关题目
给出下列定义：
①对于函数f（x），若存在x0∈R使f（x0）=x0成立，则称x0为函数f（x）的不动点；
②若函数的定义域区间与值域区间完全相同，则称该区间为函数的保值区间．
设函数f（x）=x2-2ax+a2+a（x∈R），则该函数有（ ）
①对于函数f（x），若存在x0∈R使f（x0）=x0成立，则称x0为函数f（x）的不动点；
②若函数的定义域区间与值域区间完全相同，则称该区间为函数的保值区间．
设函数f（x）=x2-2ax+a2+a（x∈R），则该函数有（ ）
| A、一个不动点和一个保值区间 |
| B、两个不动点和一个保值区间 |
| C、两个不动点和两个保值区间 |
| D、两个不动点和三个保值区间 |
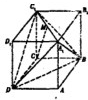如图，在长方体ABCD-A1B1C1D1中，AB=
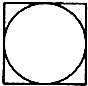如图是一个边长为1的正方形及其内切圆，现随机地向该正方形内投一粒黄豆（视为一点），则黄豆落入圆内的概率为