题目内容
求方程的质数解：p3-q5=（p+q）2．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：p，q是质数，p3-q5肯定是偶数，p+q则也为偶数，p＞q，经过验证得答案．
解答：
解：∵p3-q5=（p+q）2．有质数解，
∴p，q是质数，p3-q5肯定是偶数，p+q则也为偶数，
1，3，5，7，9，11…
验证p=7，q=3，成立，
由p3=q5+（p+q）2，令y=p3，y=q5+（p+q）2，
可判断都随着p，q的增大而增大．
即p=7，q=3，
∴p，q是质数，p3-q5肯定是偶数，p+q则也为偶数，
1，3，5，7，9，11…
验证p=7，q=3，成立，
由p3=q5+（p+q）2，令y=p3，y=q5+（p+q）2，
可判断都随着p，q的增大而增大．
即p=7，q=3，
点评：本题综合考察了方程，函数的知识．
练习册系列答案
相关题目
已知实数x，y满足
，则x2+y2+4x+6y+14的最大值为（ ）
|
| A、42 | ||
B、
| ||
C、
| ||
| D、46 |
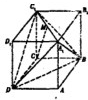如图，在长方体ABCD-A1B1C1D1中，AB=