题目内容
已知函数f(x)=alnx+
x2+x.
(1)求f(x)的单调区间;
(2)函数g(x)=
x3+x-
(x>0),求证:a=1时f(x)的图象都不在g(x)图象的上方.
| 1 |
| 2 |
(1)求f(x)的单调区间;
(2)函数g(x)=
| 2 |
| 3 |
| 1 |
| 6 |
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)求出函数的导数,通过导数的符号,判断函数的单调性.求出单调区间.
(2)构造函数υ(x)=f(x)-g(x)=lnx+
x2-(
x3+
),(x>0),通过函数的导数,求出函数的最值,通过函数的最值说明结论.
(2)构造函数υ(x)=f(x)-g(x)=lnx+
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 6 |
解答:
解:(1)f/(x)=
+x+1=
当a≥
时,f′(x)≥0,f(x)在(0,+∞)单调递增;
当a<
时,令f′(x)=0,x1,2=
,∵x>0,
又当0≤a<
时,f′(x)≥0,f(x)在(0,+∞)单调递增;---------(7分)
当a<0时,f′(x)≥0,x≥
,f′(x)<0,0<x<
,
故f(x)在(0,
)单调递减,在(
,+∞)单调递增;
综上所述:当a≥0时,f(x)在(0,+∞)单调递增;
当a<0时,f(x)在(0,
)单调递减,在(
,+∞)单调递增.
(2)令υ(x)=f(x)-g(x)=lnx+
x2-(
x3+
),(x>0),则υ/(x)=
+x-2x2=
=
.
令υ′(x)=0得x=1,当0<x<1时υ′(x)>0,
当x>1时υ′(x)<0,故υ(x)max=υ(1)=0,υ(x)≤0,
即f(x)≤g(x),
所以a=1时f(x)的图象都不在g(x)图象的上方.---------------(14分)
| a |
| x |
| x2+x+a |
| x |
当a≥
| 1 |
| 4 |
当a<
| 1 |
| 4 |
-1±
| ||
| 2 |
又当0≤a<
| 1 |
| 4 |
当a<0时,f′(x)≥0,x≥
-1+
| ||
| 2 |
-1+
| ||
| 2 |
故f(x)在(0,
-1+
| ||
| 2 |
-1+
| ||
| 2 |
综上所述:当a≥0时,f(x)在(0,+∞)单调递增;
当a<0时,f(x)在(0,
-1+
| ||
| 2 |
-1+
| ||
| 2 |
(2)令υ(x)=f(x)-g(x)=lnx+
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 6 |
| 1 |
| x |
| 1+x2-2x3 |
| x |
| (1-x)(2x2+x+1) |
| x |
令υ′(x)=0得x=1,当0<x<1时υ′(x)>0,
当x>1时υ′(x)<0,故υ(x)max=υ(1)=0,υ(x)≤0,
即f(x)≤g(x),
所以a=1时f(x)的图象都不在g(x)图象的上方.---------------(14分)
点评:本题考查函数的导数的应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
双曲线
-
=1的两个焦点为F1(-5,0),F2(5,0),其上一点M满足MF1-MF2=-8,则该双曲线的一条渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、4x+3y=0 |
| B、4x-5y=0 |
| C、3x-4y=0 |
| D、5x+3y=0 |
设函数f(x)=
,若f(a)>f(-a),则实数a的取值范围是( )
|
| A、(-1,0)∪(1,+∞) |
| B、(-∞,-1) |
| C、(1,+∞) |
| D、(-∞,-1)∪(1,+∞) |
某中学从4名男生和3名女生中推荐4人参加志愿者活动,若这4人中必须既有男生又有女生,则不同的推选法共有( )
| A、140种 | B、34种 |
| C、35种 | D、120种 |
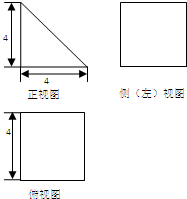 一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为
一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的表面积为