题目内容
已知函数f(x)=ln(x+1),g(x)=a(2x-x2)(a≠0,a∈R).
(1)若关于x的不等式g(x)≤bx-2的解集为{x|-2≤x≤-1},求实数a,b的值;
(2)若对于任意的x>3,f(x)≤g(x)恒成立,求实数a的取值范围.
(1)若关于x的不等式g(x)≤bx-2的解集为{x|-2≤x≤-1},求实数a,b的值;
(2)若对于任意的x>3,f(x)≤g(x)恒成立,求实数a的取值范围.
考点:指、对数不等式的解法,函数恒成立问题
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:(1)由不等式的解集,得ax2-(2a-b)x-2=0的两个根分别为-2,-1,运用韦达定理,即可得到a,b;
(2)对于任意的x>3,f(x)≤g(x)恒成立等价于a≤
=m(x)恒成立.运用导数判断m(x)的单调性,即可得到最小值,令a不大于它即可.
(2)对于任意的x>3,f(x)≤g(x)恒成立等价于a≤
| ln(x+1) |
| 2x-x2 |
解答:
解:(1)g(x)≤bx-2等价于ax2-(2a-b)x-2≥0,
由题可知ax2-(2a-b)x-2=0的两个根分别为-2,-1,
∴
=-3,-
=2,
∴a=-1,b=-5;
(2)对于任意的x>3,f(x)≤g(x)恒成立等价于a≤
=m(x)恒成立.
m'(x)=
,
令n(x)=2x-x2-2(1-x2)ln(1+x),
n'(x)=4xln(1+x)>0且n(0)=0,
∴n(x)>0,
∴m'(x)>0,m(x)在(3,+∞)上单调递增,
∴a≤m(3)=-
ln2,
即a的取值范围是(-∞,-
ln2].
由题可知ax2-(2a-b)x-2=0的两个根分别为-2,-1,
∴
| 2a-b |
| a |
| 2 |
| a |
∴a=-1,b=-5;
(2)对于任意的x>3,f(x)≤g(x)恒成立等价于a≤
| ln(x+1) |
| 2x-x2 |
m'(x)=
| 2x-x2-2(1-x2)ln(1+x) |
| (x+1)(2x-x2)2 |
令n(x)=2x-x2-2(1-x2)ln(1+x),
n'(x)=4xln(1+x)>0且n(0)=0,
∴n(x)>0,
∴m'(x)>0,m(x)在(3,+∞)上单调递增,
∴a≤m(3)=-
| 2 |
| 3 |
即a的取值范围是(-∞,-
| 2 |
| 3 |
点评:本题考查二次不等式的解法,考查不等式恒成立问题,注意运用参数分离和函数的导数判断单调性,求最值,考查运算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知函数y=f(x)图象上每个点的纵坐标保持不变,将横坐标伸长到原来的2倍,然后将整个图象沿x轴向左平移
个单位,得到的图象与y=
sinx的图象相同,则y=f(x)的函数表达式为( )
| π |
| 2 |
| 1 |
| 2 |
A、y=
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
平行于直线2x-y+1=0且与圆x2+y2=5相切的直线方程是( )
| A、2x-y+5=0 |
| B、2x-y-5=0 |
| C、2x-y±5=0 |
| D、2x+y±5=0 |
若cos(
-α)=
,α∈(-π,0),则sin(
+2α)=( )
| π |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
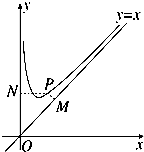 如图,函数f(x)=x+
如图,函数f(x)=x+