题目内容
已知数列{an}前n项和为Sn且Sn=3an+1,求{an}通项公式.
考点:数列的求和
专题:等差数列与等比数列
分析:当n=1时,a1=S1=3a1+1,解得a1.当n≥2时,an=Sn-Sn-1,化为2an=3an-1.利用等比数列的通项公式即可得出.
解答:
解:当n=1时,a1=S1=3a1+1,解得a1=-
.
当n≥2时,an=Sn-Sn-1=3an+1-(3an-1+1),化为2an=3an-1.
∴数列{an}是等比数列,
∴an=-
•(
)n-1.
| 1 |
| 2 |
当n≥2时,an=Sn-Sn-1=3an+1-(3an-1+1),化为2an=3an-1.
∴数列{an}是等比数列,
∴an=-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了递推式的应用、等比数列的通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
用反证法证明命题:“已知a,b∈N,若ab不能被7整除,则a与b都不能被7整除”时,假设的内容应为( )
| A、a,b都能被7整除 |
| B、a,b不都能被7整除 |
| C、a,b至少有一个能被7整除 |
| D、a,b至多有一个能被7整除 |
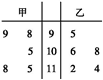 在某中学举行的跳高比赛选拨赛中,甲和乙进行了5次比赛,他们的成绩用如图所示的茎叶图表示,则下列说法正确的是( )
在某中学举行的跳高比赛选拨赛中,甲和乙进行了5次比赛,他们的成绩用如图所示的茎叶图表示,则下列说法正确的是( )| A、甲的平均成绩比乙的平均成绩高,甲比乙成绩稳定 |
| B、甲的平均成绩比乙的平均成绩低,乙比甲成绩稳定 |
| C、甲的平均成绩与乙的平均成绩一样,但甲比乙成绩稳定 |
| D、甲的平均成绩与乙的平均成绩一样,但乙比甲成绩稳定 |
以下条件表达式正确的是( )
| A、1<x<2 | B、x><1 |
| C、x<>1 | D、x≤1 |
已知函数f(x)=4x-2x+1+1,函数g(x)=asin(
x)-2a+2(a>0),若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是( )
| π |
| 6 |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
高三(1)班从4名男生和3名女生中推荐4人参加学校组织社会公益活动,若选出的4人中既有男生又有女生,则不同的选法共有( )
| A、34种 | B、35种 |
| C、120种 | D、140种 |
为了了解学生对新课程改革的满意情况,有关教育部门对某中学的100名学生随机进行了调查,得到如下的统计表:
已知在全部100名学生中随机抽取1人对课程改革满意的概率为
.参照附表,得到的正确结论是( )
| 满 意 | 不满意 | 合 计 | |
| 男 生 | 50 | ||
| 女 生 | 15 | ||
| 合 计 | 100 |
| 4 |
| 5 |
| A、在犯错误的概率不超过0.1%的情况下,有把握说学生对新课程改革工作的满意情况与性别有关 |
| B、在犯错误的概率不超过0.1%的情况下,有把握说学生对新课程改革工作的满意情况与性别无关 |
| C、在犯错误的概率不超过0.5%的情况下,有把握说学生对新课程改革工作的满意情况与性别有关 |
| D、在犯错误的概率不超过0.5%的情况下,有把握说学生对新课程改革工作的满意情况与性别无关 |