题目内容
已知数列{an}的前n项和为Sn,且Sn+an=1(n∈N*),等差数列{bn}的公差为正数,其前n项和为Tn,T3=15,且b1,
,b3成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若cn=
,求数列{cn}的前n项和Pn.
| 1 |
| a2 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若cn=
| 3 |
| bnbn+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(I)Sn+an=1,可得当n=1时,2a1=1,当n≥2时,an=Sn-Sn-1,化为2an=an-1.利用等比数列的通项公式即可得出.
(II)由b1,
,b3成等比数列,可得(
)2=b1b3,b1(b1+2d)=16,又T3=15,可得b1+d=5,联立解出即可.bn=3n-1.cn=
=
-
,利用“裂项求和”即可得出.
(II)由b1,
| 1 |
| a2 |
| 1 |
| a2 |
| 3 |
| bnbn+1 |
| 1 |
| 3n-1 |
| 1 |
| 3n+2 |
解答:
解:(I)∵Sn+an=1,
∴当n=1时,2a1=1,∴a1=
;
当n≥2时,an=Sn-Sn-1=(1-an)-(1-an-1),化为2an=an-1.
∴数列{an}是等比数列,an=(
)n.
(II)∵b1,
,b3成等比数列,
∴(
)2=b1b3,
∴b1(b1+2d)=16,
又T3=15,∴3b1+
d=15,化为b1+d=5,
联立
,又d>0,解得
.
∴bn=2+3(n-1)=3n-1.
∴cn=
=
=
-
,
∴数列{cn}的前n项和Pn=(
-
)+(
-
)+…+(
-
)
=
-
=
.
∴当n=1时,2a1=1,∴a1=
| 1 |
| 2 |
当n≥2时,an=Sn-Sn-1=(1-an)-(1-an-1),化为2an=an-1.
∴数列{an}是等比数列,an=(
| 1 |
| 2 |
(II)∵b1,
| 1 |
| a2 |
∴(
| 1 |
| a2 |
∴b1(b1+2d)=16,
又T3=15,∴3b1+
| 3×2 |
| 2 |
联立
|
|
∴bn=2+3(n-1)=3n-1.
∴cn=
| 3 |
| bnbn+1 |
| 3 |
| (3n-1)(3n+2) |
| 1 |
| 3n-1 |
| 1 |
| 3n+2 |
∴数列{cn}的前n项和Pn=(
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 8 |
| 1 |
| 3n-1 |
| 1 |
| 3n+2 |
=
| 1 |
| 2 |
| 1 |
| 3n+2 |
=
| 3n |
| 6n+4 |
点评:本题考查了等差数列与等比数列的通项公式、“裂项求和”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
用反证法证明命题:“已知a,b∈N,若ab不能被7整除,则a与b都不能被7整除”时,假设的内容应为( )
| A、a,b都能被7整除 |
| B、a,b不都能被7整除 |
| C、a,b至少有一个能被7整除 |
| D、a,b至多有一个能被7整除 |
若(1+2ai)i=1-bi,其中a、b∈R,i是虚数单位,则|a+bi|=( )
A、
| ||||
| B、5 | ||||
C、
| ||||
D、
|
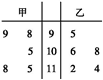 在某中学举行的跳高比赛选拨赛中,甲和乙进行了5次比赛,他们的成绩用如图所示的茎叶图表示,则下列说法正确的是( )
在某中学举行的跳高比赛选拨赛中,甲和乙进行了5次比赛,他们的成绩用如图所示的茎叶图表示,则下列说法正确的是( )| A、甲的平均成绩比乙的平均成绩高,甲比乙成绩稳定 |
| B、甲的平均成绩比乙的平均成绩低,乙比甲成绩稳定 |
| C、甲的平均成绩与乙的平均成绩一样,但甲比乙成绩稳定 |
| D、甲的平均成绩与乙的平均成绩一样,但乙比甲成绩稳定 |