题目内容
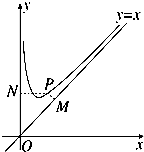 如图,函数f(x)=x+
如图,函数f(x)=x+
| ||
| x |
(1)证明:|PM|•|PN|为定值;
(2)O为坐标原点,求四边形OMPN面积的最小值.
考点:函数恒成立问题,函数的图象
专题:计算题,函数的性质及应用
分析:(1)根据条件,设出P的坐标,求出|PM|•|PN|,判断是否为定值即可.
(2)根据条件将四边形OMPN分解为两个三角形OPM和OPN,分别表示出两个三角形的面积,利用基本不等式的性质进行求最值.
(2)根据条件将四边形OMPN分解为两个三角形OPM和OPN,分别表示出两个三角形的面积,利用基本不等式的性质进行求最值.
解答:
解:(1)设P的坐标为(m,n)(m>0),则有n=m+
,
即有n-m=
,
由点到直线的距离公式得|PM|=
=
,|PN|=m,
即|PM|•|PN|=1,
即|PM|•|PN|为定值1;
(2)由题意可设M(t,t),知N(0,n),
由PM与直线y=x垂直,知kPM=-1,
即
=-1,
又n=m+
解得t=m+
,
故|OM|=
t=
m+
,
∴S△OPM=
•|OM|•|PM|=
(
m+
)•
=
(
+
),
S△OPN=
•|ON|•|PN|=
•mn=
(m2+
),
∴SOMPN=S△OPM+S△OPN=
(2
+m2+
)≥
(2
+2)=
+1,
当且仅当m2=
,即m=1时等号成立,
故四边形面积有最小值
+1.
| ||
| m |
即有n-m=
| ||
| m |
由点到直线的距离公式得|PM|=
| |n-m| | ||
|
| 1 |
| m |
即|PM|•|PN|=1,
即|PM|•|PN|为定值1;
(2)由题意可设M(t,t),知N(0,n),
由PM与直线y=x垂直,知kPM=-1,
即
| n-t |
| m-t |
又n=m+
| ||
| m |
解得t=m+
| ||
| 2m |
故|OM|=
| 2 |
| 2 |
| 1 |
| m |
∴S△OPM=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| m |
| 1 |
| m |
| 1 |
| 2 |
| 2 |
| 1 |
| m2 |
S△OPN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴SOMPN=S△OPM+S△OPN=
| 1 |
| 2 |
| 2 |
| 1 |
| m2 |
| 1 |
| 2 |
| 2 |
| 2 |
当且仅当m2=
| 1 |
| m2 |
故四边形面积有最小值
| 2 |
点评:本题主要考查曲线和方程,以及点到直线的距离公式的应用,利用基本不等式是解决本题的关键,涉及的知识点较多,综合性较强,运算量较大.

练习册系列答案
相关题目
为了了解学生对新课程改革的满意情况,有关教育部门对某中学的100名学生随机进行了调查,得到如下的统计表:
已知在全部100名学生中随机抽取1人对课程改革满意的概率为
.参照附表,得到的正确结论是( )
| 满 意 | 不满意 | 合 计 | |
| 男 生 | 50 | ||
| 女 生 | 15 | ||
| 合 计 | 100 |
| 4 |
| 5 |
| A、在犯错误的概率不超过0.1%的情况下,有把握说学生对新课程改革工作的满意情况与性别有关 |
| B、在犯错误的概率不超过0.1%的情况下,有把握说学生对新课程改革工作的满意情况与性别无关 |
| C、在犯错误的概率不超过0.5%的情况下,有把握说学生对新课程改革工作的满意情况与性别有关 |
| D、在犯错误的概率不超过0.5%的情况下,有把握说学生对新课程改革工作的满意情况与性别无关 |
“a=b-4”是“直线y=x+2与圆(x-a)2+(y-b)2=2相切”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知向量
=(3,-1),
=(k,7),若
+
与3
-2
平行,则实数k等于( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、-21 | B、21 | C、2 | D、0 |
命题p:对任意x∈[0,+∞),(log32)x≤1,则¬p为( )
| A、存在x0∈[0,+∞),(log32)x0≤1,是假命题 |
| B、对任意x∈[0,+∞),(log32)x≤1,是真命题 |
| C、存在x0∈[0,+∞),(log32)x0>1,是假命题 |
| D、对任意x∈[0,+∞),(log32)x>1,是真命题 |