题目内容
某批次的某种灯泡共200个,对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于500天的灯泡是优等品,寿命小于300天的灯泡是次品,其余的灯泡是正品.
(Ⅰ)根据频率分布表中的数据,写出a,b,c的值;
(Ⅱ)某人从这200个灯泡中随机地购买了1个,求此灯泡恰好不是次品的概率;
(Ⅲ)某人从这批灯泡中随机地购买了n(n∈N*)个,如果这n个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求n的最小值.
| 寿命(天) | 频数 | 频率 |
| [100,200) | 10 | 0.05 |
| [200,300) | 30 | a |
| [300,400) | 70 | 0.35 |
| [400,500) | b | 0.15 |
| [500,600) | 60 | c |
| 合计 | 200 | 1 |
(Ⅱ)某人从这200个灯泡中随机地购买了1个,求此灯泡恰好不是次品的概率;
(Ⅲ)某人从这批灯泡中随机地购买了n(n∈N*)个,如果这n个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求n的最小值.
考点:古典概型及其概率计算公式,分层抽样方法
专题:概率与统计
分析:(Ⅰ)由频率分布表中的数据,求出a、b、c的值.
(Ⅱ)根据频率分布表中的数据,求出此人购买的灯泡恰好不是次品的概率.
(Ⅲ)由这批灯泡中优等品、正品和次品的比例数,再按分层抽样方法,求出购买灯泡数n的最小值.
(Ⅱ)根据频率分布表中的数据,求出此人购买的灯泡恰好不是次品的概率.
(Ⅲ)由这批灯泡中优等品、正品和次品的比例数,再按分层抽样方法,求出购买灯泡数n的最小值.
解答:
解:(Ⅰ)根据频率分布表中的数据,得
a=
=0.15,
b=200-(10+30+70+60)=30,
c=
=0.3.
(Ⅱ)设“此人购买的灯泡恰好不是次品”为事件A.
由表可知:这批灯泡中优等品有60个,正品有100个,次品有40个,
所以此人购买的灯泡恰好不是次品的概率为P(A)=
=
.
(Ⅲ)由(Ⅱ)得这批灯泡中优等品、正品和次品的比例为60:100:40=3:5:2.
所以按分层抽样法,购买灯泡数 n=3k+5k+2k=10k(k∈N*),
所以n的最小值为10.
a=
| 30 |
| 200 |
b=200-(10+30+70+60)=30,
c=
| 60 |
| 200 |
(Ⅱ)设“此人购买的灯泡恰好不是次品”为事件A.
由表可知:这批灯泡中优等品有60个,正品有100个,次品有40个,
所以此人购买的灯泡恰好不是次品的概率为P(A)=
| 100+60 |
| 200 |
| 4 |
| 5 |
(Ⅲ)由(Ⅱ)得这批灯泡中优等品、正品和次品的比例为60:100:40=3:5:2.
所以按分层抽样法,购买灯泡数 n=3k+5k+2k=10k(k∈N*),
所以n的最小值为10.
点评:本题考查了分层抽样方法以及古典概型的概率及其应用问题,解题时应根据题目中的表格求出未知的量,利用概率的知识解答,是综合题.

练习册系列答案
相关题目
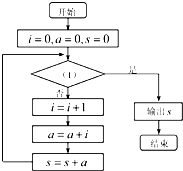 在数列{an}中,a1=1,an=an-1+n,n≥2,为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是
在数列{an}中,a1=1,an=an-1+n,n≥2,为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是