题目内容
设a,b为正实数,现有下列命题:
①若|
-
|=1,则|a-b|<1;
②若
-
=1,则a-b<1;
③若a2-b2=1,则a-b<1;
④若|a3-b3|=1,则|a-b|<1.
其中的真命题的个数为 .
①若|
| a |
| b |
②若
| 1 |
| b |
| 1 |
| a |
③若a2-b2=1,则a-b<1;
④若|a3-b3|=1,则|a-b|<1.
其中的真命题的个数为
考点:不等式的基本性质
专题:不等式的解法及应用
分析:①取a=4,b=1满足条件|
-
|=1,即可判断出;
②取a=3,b=
满足条件
-
=1,即可判断出;
③由已知可得0<a-b<a+b,可得a-b=
<1;
④由已知不妨设a>b>0,可得a2+ab+b2>a2-2ab+b2>0,进而得到a3-b3>(a-b)3>0,即可判断出.
| a |
| b |
②取a=3,b=
| 3 |
| 4 |
| 1 |
| b |
| 1 |
| a |
③由已知可得0<a-b<a+b,可得a-b=
| 1 |
| a+b |
④由已知不妨设a>b>0,可得a2+ab+b2>a2-2ab+b2>0,进而得到a3-b3>(a-b)3>0,即可判断出.
解答:
解:①若|
-
|=1,取a=4,b=1满足条件,而|a-b|=3>1,因此①不正确;
②若
-
=1,取a=3,b=
满足条件,则a-b>1,因此不正确;
③∵a2-b2=1,∴(a-b)(a+b)=1,
∵a>0,b>0,∴0<a-b<a+b,
∴a-b=
<1,因此正确;
④∵|a3-b3|=1,a>0,b>0,
∴a≠b,不妨设a>b>0.
∴a2+ab+b2>a2-2ab+b2>0,
∴(a-b)(a2+ab+b2)>(a-b)(a-b)2
即a3-b3>(a-b)3>0.
∴1=|a3-b3|>(a-b)3>0,
∴0<a-b<1,
即|a-b|<1.因此正确.
综上可知:只有③④正确.
故答案为:2.
| a |
| b |
②若
| 1 |
| b |
| 1 |
| a |
| 3 |
| 4 |
③∵a2-b2=1,∴(a-b)(a+b)=1,
∵a>0,b>0,∴0<a-b<a+b,
∴a-b=
| 1 |
| a+b |
④∵|a3-b3|=1,a>0,b>0,
∴a≠b,不妨设a>b>0.
∴a2+ab+b2>a2-2ab+b2>0,
∴(a-b)(a2+ab+b2)>(a-b)(a-b)2
即a3-b3>(a-b)3>0.
∴1=|a3-b3|>(a-b)3>0,
∴0<a-b<1,
即|a-b|<1.因此正确.
综上可知:只有③④正确.
故答案为:2.
点评:本题考查了不等式的性质、取特殊值否定一个命题的方法等基础知识与基本技能方法,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知实数x∈[1,10],执行如图所示的程序框图,则输出x的值不小于55的概率为( )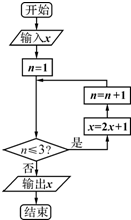

A、
| ||
B、
| ||
C、
| ||
D、
|
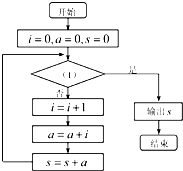 在数列{an}中,a1=1,an=an-1+n,n≥2,为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是
在数列{an}中,a1=1,an=an-1+n,n≥2,为计算这个数列前10项的和S,现给出该问题算法的程序框图(如图所示),则图中判断框(1)处合适的语句是