题目内容
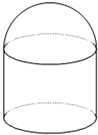如图，储油灌的表面积S为定值，它的上部是半球，下部是圆柱，半球的半径等于圆柱底面半径．（1）试用半径r表示出储油灌的容积V，并写出r的范围．
（2）当圆柱高h与半径r的比为多少时，储油灌的容积V最大？
考点：导数在最大值、最小值问题中的应用
专题：应用题,导数的综合应用
分析：（1）由表面积S为定值，用r表示出h，可得储油灌的容积V及r的范围；
（2）求导函数，确定函数的极大值即最大值，即可得出结论．
（2）求导函数，确定函数的极大值即最大值，即可得出结论．
解答：
解：（1）∵S=2πr2+2πrh+πr2=3πr2+2πrh，∴h=
，…（3分）
∴V=
πr3+πr2h=
-
πr3 (0＜r＜
)； …（7分）
（2）∵V′=
-
πr2，令V'=0，得r=
，列表
…（11分）
∴当r=
时，体积V取得最大值，此时h=
，
∴h：r=1：1．…（13分）
答：储油灌容积V=
-
πr3 (0＜r＜
)，当h：r=1：1时容积V取得最大值．…（15分）
| S-3πr2 |
| 2πr |
∴V=
| 2 |
| 3 |
| rS |
| 2 |
| 5 |
| 6 |
| ||
| 3π |
（2）∵V′=
| S |
| 2 |
| 5 |
| 2 |
| ||
| 5π |
| r | (0，
|
|
(
| ||||||||||||||||
| V'（r） | + | 0 | - | ||||||||||||||||
| V（r） | ↗ | 极大值即最大值 | ↘ |
∴当r=
| ||
| 5π |
| ||
| 5π |
∴h：r=1：1．…（13分）
答：储油灌容积V=
| rS |
| 2 |
| 5 |
| 6 |
| ||
| 3π |
点评：本题考查导数知识的运用，考查函数的最值，考查学生利用数学知识解决实际问题的能力，确定函数解析式是关键．
练习册系列答案
相关题目
将函数y=sin（2x+φ）的图象沿x轴向左平移
个单位后，得到一个关于y轴对称的图象，则φ的一个可能取值为（ ）
| π |
| 6 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
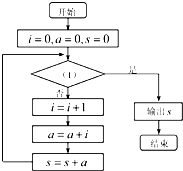在数列{an}中，a1=1，an=an-1+n，n≥2，为计算这个数列前10项的和S，现给出该问题算法的程序框图（如图所示），则图中判断框（1）处合适的语句是