题目内容
 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| OF |
| FB |
| AB |
| BF |
(Ⅰ)求椭圆E的方程;
(Ⅱ)若点A与椭圆上的另一点C(非右顶点)关于直线l对称,直线l上一点N(0,y0)满足
| NA |
| NC |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由已知条件得A(-a,0),B(0,b),F(1,0),由
•
=
•
,推导出b2-a-1=0,由此能求出椭圆方程.
(Ⅱ)先求出l的方程,可得N的坐标,再利用
•
=0,即可求点C的坐标.
| OF |
| FB |
| AB |
| BF |
(Ⅱ)先求出l的方程,可得N的坐标,再利用
| NA |
| NC |
解答:
解:(Ⅰ)由题意,A(-a,0),B(0,b),F(1,0),
∵
•
=
•
,
∴b2-a-1=0,
∵b2=a2-1,∴a2-a-2=0,解得a=2,
∴a2=4,b2=3,
∴椭圆E的方程为
+
=1;
(Ⅱ)设C(x1,y1)(y1≠0),且A(-2,0),则AC的中点M(
,
),
由已知kAC=
,则kl=-
,
∴l:y-
=-
(x-
),
令x=0,则y0=
=-
,
即N(0,-
),
∴
•
=(-2,
)•(x1,
)=-2x1+
=0,
∴7x12+96x1-28=0
∴x1=
(x1=-14舍去),
∴y1=±
,
∴C(
,±
).
∵
| OF |
| FB |
| AB |
| BF |
∴b2-a-1=0,
∵b2=a2-1,∴a2-a-2=0,解得a=2,
∴a2=4,b2=3,
∴椭圆E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设C(x1,y1)(y1≠0),且A(-2,0),则AC的中点M(
| x1-2 |
| 2 |
| y1 |
| 2 |
由已知kAC=
| y1 |
| x1+2 |
| x1+2 |
| y1 |
∴l:y-
| y1 |
| 2 |
| x1+2 |
| y1 |
| x1-2 |
| 2 |
令x=0,则y0=
| x12-4+y12 |
| 2y1 |
| y1 |
| 6 |
即N(0,-
| y1 |
| 6 |
∴
| NA |
| NC |
| y1 |
| 6 |
| 7y1 |
| 6 |
| 7y12 |
| 36 |
∴7x12+96x1-28=0
∴x1=
| 2 |
| 7 |
∴y1=±
| 12 |
| 7 |
∴C(
| 2 |
| 7 |
| 12 |
| 7 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 已知ω>0,|φ|<
已知ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
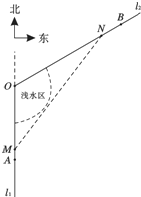 某港湾的平面示意图如图所示,O,A,B分别是海岸线l1,l2上的三个集镇,A位于O的正南方向6km处,B位于O的北偏东60°方向10km处.
某港湾的平面示意图如图所示,O,A,B分别是海岸线l1,l2上的三个集镇,A位于O的正南方向6km处,B位于O的北偏东60°方向10km处.