题目内容
已知
,
的夹角为120°,|
|=2,|
|=3,记|
=3
-2
,
=2
+k
.
(1)若
⊥
,求实数k的值.
(2)是否存在实数k,使得
∥
?说明理由.
| a |
| b |
| a |
| b |
| m |
| a |
| b |
| n |
| a |
| b |
(1)若
| m |
| n |
(2)是否存在实数k,使得
| m |
| n |
考点:平面向量的综合题
专题:计算题,平面向量及应用
分析:(1)由
⊥
可得
•
=0,即(3
-2
)•(2
+k
)=0,从而求k;
(2)由
∥
,则
=λ
,即3
-2
=2λ
+kλ
,即2λ=3,2=-kλ,从而求k.
| m |
| n |
| m |
| n |
| a |
| b |
| a |
| b |
(2)由
| m |
| n |
| m |
| n |
| a |
| b |
| a |
| b |
解答:
解:(1)∵
⊥
,
∴
•
=0,
即(3
-2
)•(2
+k
)=0,
即6|
|2+(3k-4)|
||
|cos120°-2k|
|2=0,
即24+(3k-4)×2×3×(-
)-18k=0,
解得,k=
.
(2)若
∥
,则
=λ
,
即3
-2
=2λ
+kλ
,
即2λ=3,2=-kλ,
解得,λ=
,k=-
.
| m |
| n |
∴
| m |
| n |
即(3
| a |
| b |
| a |
| b |
即6|
| a |
| a |
| b |
| b |
即24+(3k-4)×2×3×(-
| 1 |
| 2 |
解得,k=
| 4 |
| 3 |
(2)若
| m |
| n |
| m |
| n |
即3
| a |
| b |
| a |
| b |
即2λ=3,2=-kλ,
解得,λ=
| 3 |
| 2 |
| 4 |
| 3 |
点评:本题考查了平面向量垂直与平行的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列说法正确的是( )
| A、“f(0)=0”是“函数f(x)是奇函数”的充要条件 | ||||||||||||||||||
B、“向量
| ||||||||||||||||||
| C、“?x∈R,x2+1>0”的否定是“?x0∈R,x02+1<0” | ||||||||||||||||||
D、“若a=
|
已知集合A={x|2x2-3x-2<0},集合B={x|
≥1},则A∩B=( )
| 2x+1 |
| x-1 |
A、(-
| ||
| B、(1,2) | ||
| C、[1,2) | ||
D、(-
|
已知函数f(x)=2ax+
(a∈R).
(1)当0<a≤
时,试判断f(x)在(0,1]上的单调性并用定义证明你的结论;
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
| 1 |
| x |
(1)当0<a≤
| 1 |
| 2 |
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
已知实数x、y满足
,则目标函数z=x2+y2的最小值为( )
|
A、
| ||
| B、2 | ||
| C、1 | ||
| D、5 |
下列函数是奇函数的是( )
A、y=x -
| ||
| B、y=2x2-3 | ||
C、y=x
| ||
| D、y=x2,x∈[0,1] |
如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=
AB且SA=SB=SC=AB=BC,则异面直线AC与BE所成的角为( ) 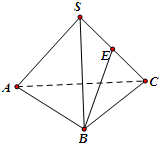
| 3 |

| A、30° | B、45° |
| C、60° | D、90° |
函数y=log2|x|的大致图象是( )
A、 |
B、 |
C、 |
D、 |