题目内容
如图，在三棱锥S-ABC中，E为棱SC的中点，若AC=
AB且SA=SB=SC=AB=BC，则异面直线AC与BE所成的角为（ ）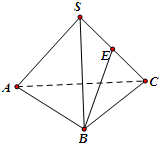 
| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：取SA的中点F，连接EF，BF，因为AC∥EF，所以BEF（或其补角）为异面直线AC与BE所成的角，求出三角形的三边，即可求出异面直线AC与BE所成的角．
解答：
解：取SA的中点F，连接EF，BF，
∵E为棱SC的中点，
∴EF∥AC，
∴∠BEF（或其补角）为异面直线AC与BE所成的角，
∵AC=
AB且SA=SB=SC=AB=BC，设AB=2，
∴BE=EF=BF=
，
∴∠BEF=60°．
故选：C．
解：取SA的中点F，连接EF，BF，∵E为棱SC的中点，
∴EF∥AC，
∴∠BEF（或其补角）为异面直线AC与BE所成的角，
∵AC=
| 3 |
∴BE=EF=BF=
| 3 |
∴∠BEF=60°．
故选：C．
点评：本题考查异面直线及其所成的角，考查学生的计算能力和转化能力，正确作出异面直线及其所成的角是关键．
练习册系列答案
相关题目
把1+（1+x）+（1+x）2+…+（1+x）n展开成关于x的多项式，其各项系数和为an，则an=（ ）
| A、2n+1-1 |
| B、2n-1 |
| C、2n+2-1 |
| D、与x有关 |
已知函数y=f（x）的图象在区间[a，b]上是连续不断的，且满足f（a）•f（b）＜0（a，b∈R，a＜b），则函数f（x）在（a，b）内（ ）
| A、无零点 |
| B、有且只有一个零点 |
| C、至少有一个零点 |
| D、无法确定有无零点 |
在边长为4的正方形ABCD中，AC与BD相交于O．减去△AOB，将剩下部分沿OC、OD折叠，使OA、OB重合，则以A（B），C，D，O为顶点的四面体的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
若数列{an}的通项公式为an=
，其前n项和为
，则n为（ ）
| 1 |
| n2+3n+2 |
| 7 |
| 18 |
| A、5 | B、6 | C、7 | D、8 |