Question

已知椭圆C：

x2

a2

+

y2

b2

=1（a＞b＞0）的长轴长是短轴长的

3

倍，F₁，F₂是它的左，右焦点．
（1）若P∈C，且

PF1

•

PF2

=0，|PF₁|•|PF₂|=4，求F₁，F₂的坐标；
（2）在（1）的条件下，过动点Q作以F₂为圆心、以1为半径的圆的切线QM（M是切点），且使|QF₁|=

2

|QM|，求动点Q的轨迹方程．

Answer 1

考点：轨迹方程

专题：圆锥曲线中的最值与范围问题

分析：（1）依题意知a=

3

b，（|PF₁|+|PF₂|）²=8b²+8=4a²，由此能求出F₁（-2，0），F₂（2，0）．
（2）由已知|QF₂|=

2

|QM|，|QM|²=|QF₂|²-1，|QF₁|²=2（|QF₂|²-1），设Q（x，y），由此能求出动点Q的轨迹方程．

解答： 解：（1）依题意知a=

3

b，①
∵

PF1

•

PF2

=0，∴PF₁⊥PF₂，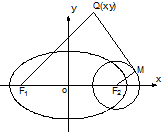
∴|PF1|2+|PF2|2=（2c）²=4（a²-b²）=8b²，
又P∈C，由椭圆定义得|PF₁|+|PF₂|=2a，
（|PF₁|+|PF₂|）²=8b²+8=4a²，②
由①②得a²=6，b²=2，∴c=2，
∴F₁（-2，0），F₂（2，0）．
（2）由已知|QF₂|=

2

|QM|，
即|QF1|2=2|QM|2，
∵QM是圆F₂的切线，
∴|QM|²=|QF₂|²-1，
∴|QF₁|²=2（|QF₂|²-1），
设Q（x，y），则（x+2）²+y²=2[（x-2）²+y²-1]，
即（x-6）²+y²=34，
综上所述，所求动点Q的轨迹方程为：（x-6）²+y²=34．

点评：本题考查椭圆的焦点坐标的求法，考查动点的轨迹方程的求法，解题时要认真审题，注意函数与方程思想的合理运用．