题目内容
下列函数是奇函数的是( )
A、y=x -
| ||
| B、y=2x2-3 | ||
C、y=x
| ||
| D、y=x2,x∈[0,1] |
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据函数的奇偶性的定义即可得到结论.
解答:
解:A.y=x -
=
的定义域为{x|x≠0},f(-x)=
=-
=-f(x),则f(x)是奇函数.满足条件.
B.f(-x)=2x2-3=f(x),则f(x)是偶函数.
C.函数的定义域为[0,+∞),定义域关于原点不对称,为非奇非偶函数.
D.函数的定义域为[0,1],定义域关于原点不对称,为非奇非偶函数.
故选:A
| 1 |
| 3 |
| 1 | |||
|
| 1 | |||
|
| 1 | |||
|
B.f(-x)=2x2-3=f(x),则f(x)是偶函数.
C.函数的定义域为[0,+∞),定义域关于原点不对称,为非奇非偶函数.
D.函数的定义域为[0,1],定义域关于原点不对称,为非奇非偶函数.
故选:A
点评:本题主要考查函数的奇偶性的判断,根据函数奇偶性的定义是解决本题的关键.

练习册系列答案
相关题目
已知函数y=f(x)的图象在区间[a,b]上是连续不断的,且满足f(a)•f(b)<0(a,b∈R,a<b),则函数f(x)在(a,b)内( )
| A、无零点 |
| B、有且只有一个零点 |
| C、至少有一个零点 |
| D、无法确定有无零点 |
函数f(x)=lgx+x的零点所在的区间为( )
A、(
| ||||
B、(0,
| ||||
C、(
| ||||
| D、(1,2) |
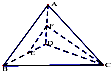 如图,在三棱锥A-BCD中,BC=CD=DB,AB=AC=AD;E,F为棱BD,AD的中点,若EF⊥CF,则直线BD与平面ACD所成的角为
如图,在三棱锥A-BCD中,BC=CD=DB,AB=AC=AD;E,F为棱BD,AD的中点,若EF⊥CF,则直线BD与平面ACD所成的角为