题目内容
已知函数f(x)=2ax+
(a∈R).
(1)当0<a≤
时,试判断f(x)在(0,1]上的单调性并用定义证明你的结论;
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
| 1 |
| x |
(1)当0<a≤
| 1 |
| 2 |
(2)对于任意的x∈(0,1],使得f(x)≥6恒成立,求实数a的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)利用定义证明即可,
(2)利用导数判断函数的最值,需要分类讨论,问题得以解决
(2)利用导数判断函数的最值,需要分类讨论,问题得以解决
解答:
解:(1)f(x)在(0,1]上的单调性递减,
理由如下:
设x1,x2∈(0,1],且x1<x2,
则f(x1)-f(x2)=2ax1+
-2ax2-
=2a(x1-x2)+
=
(1-2ax1x2),
∵x1,x2∈(0,1],且x1<x2,0<a≤
,
∴x2-x1>0,0<x1•x2<1,0<2ax1x2<1,1-2ax1x2>0,
∴f(x1)-f(x2)>0,
∴f(x)在(0,1]上的单调性递减,
(2)∵f(x)=2ax+
,
∴f′(x)=2a-
=
,
①当a≤0时,f′(x)<0,
∴函数f(x)在(0,1]单调递减,
∴f(x)min=f(1)=2a≥6,
解得a≤3,
∴a≤0时,对于任意的x∈(0,1],使得f(x)≥6恒成立,
②当a>0时,
令f′(x)=0,解得x=
,
当f′(x)>0,即x>
,函数f(x)单调递增,
当f′(x)<0,即0<x<
,函数f(x)单调递减,
当
≥1时,即0<a≤
时,f(x)在(0,1]上的单调性递减,
∴f(x)min=f(1)=2a≥6恒成立
解得a≤3,
当
<1时,即a>
时,
∴f(x)在(0,
]上的单调递减,在(
,1)上单调递增,
∴f(x)min=f(
)=2a•
+
≥6恒成立,
解得a≥
,
综上所述实数a的取值范围为(-∞,
]∪[
,+∞)
理由如下:
设x1,x2∈(0,1],且x1<x2,
则f(x1)-f(x2)=2ax1+
| 1 |
| x1 |
| 1 |
| x2 |
| x2-x1 |
| x1x2 |
| x2-x1 |
| x1x2 |
∵x1,x2∈(0,1],且x1<x2,0<a≤
| 1 |
| 2 |
∴x2-x1>0,0<x1•x2<1,0<2ax1x2<1,1-2ax1x2>0,
∴f(x1)-f(x2)>0,
∴f(x)在(0,1]上的单调性递减,
(2)∵f(x)=2ax+
| 1 |
| x |
∴f′(x)=2a-
| 1 |
| x2 |
| 2ax2-1 |
| x2 |
①当a≤0时,f′(x)<0,
∴函数f(x)在(0,1]单调递减,
∴f(x)min=f(1)=2a≥6,
解得a≤3,
∴a≤0时,对于任意的x∈(0,1],使得f(x)≥6恒成立,
②当a>0时,
令f′(x)=0,解得x=
|
当f′(x)>0,即x>
|
当f′(x)<0,即0<x<
|
当
|
| 1 |
| 2 |
∴f(x)min=f(1)=2a≥6恒成立
解得a≤3,
当
|
| 1 |
| 2 |
∴f(x)在(0,
|
|
∴f(x)min=f(
|
|
| 2a |
解得a≥
| 9 |
| 2 |
综上所述实数a的取值范围为(-∞,
| 1 |
| 2 |
| 9 |
| 2 |
点评:本题主要考查了函数的单调性和导数与函数的最值问题,以及求参数的取值范围,属于中档题

练习册系列答案
相关题目
已知集合A={x|x2-3x-4≤0},B={x|x=
,x∈Z,k∈Z},则A∩B=( )
| 3 |
| 2k-1 |
| A、{-1,1} |
| B、{-1,1,3} |
| C、{-3,-1,1} |
| D、{-3,-1,1,3} |
已知函数y=f(x)的图象在区间[a,b]上是连续不断的,且满足f(a)•f(b)<0(a,b∈R,a<b),则函数f(x)在(a,b)内( )
| A、无零点 |
| B、有且只有一个零点 |
| C、至少有一个零点 |
| D、无法确定有无零点 |
 已知函数f(x)=
已知函数f(x)=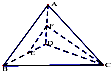 如图,在三棱锥A-BCD中,BC=CD=DB,AB=AC=AD;E,F为棱BD,AD的中点,若EF⊥CF,则直线BD与平面ACD所成的角为
如图,在三棱锥A-BCD中,BC=CD=DB,AB=AC=AD;E,F为棱BD,AD的中点,若EF⊥CF,则直线BD与平面ACD所成的角为