题目内容
已知a、b是不相等的正数,且a、x、y、b成等差数列,a、m、n、b成等比数列,则下列关系成立的是( )
| A、x+y>m+n |
| B、x+y=m+n |
| C、x+y<m+n |
| D、不能确定 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:利用条件,推出q>0,再作差,即可得出结论.
解答:
解:设a,x,y,b依次成等差数列的公差为d,则:x=a+d,y=a+2d,b=a+3d;
a,m,n,b依次成等比数列的公比为q,则:m=aq,n=aq2,b=aq3,所以有a+3d=aq3得到3d=aq3-a;
因为x+y=2a+3d=2a+aq3-a=a(1+q3)=a(1+q)(1+q+q2)m+n=aq+aq2=aq(1+q),
所以x+y-(m+n)=a(1+q)(1+q+q2)-aq(1+q)=a(1+q)(1+q+q2-q)=a(1+q)(1+q2),
因为a>0,b>0,所以b=aq3>0,所以q>0,
所以1+q>0,1+q2>0,所以x+y-(m+n)=a(1+q)(1+q2)>0,
所以x+y>m+n.
故选:A.
a,m,n,b依次成等比数列的公比为q,则:m=aq,n=aq2,b=aq3,所以有a+3d=aq3得到3d=aq3-a;
因为x+y=2a+3d=2a+aq3-a=a(1+q3)=a(1+q)(1+q+q2)m+n=aq+aq2=aq(1+q),
所以x+y-(m+n)=a(1+q)(1+q+q2)-aq(1+q)=a(1+q)(1+q+q2-q)=a(1+q)(1+q2),
因为a>0,b>0,所以b=aq3>0,所以q>0,
所以1+q>0,1+q2>0,所以x+y-(m+n)=a(1+q)(1+q2)>0,
所以x+y>m+n.
故选:A.
点评:本题考查等差数列的性质,考查作差比较法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列函数中,值域为(0,+∞)的是( )
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
如表是某城市2001-2010年月平均气温(华氏F):
若用x表示月份,y表示平均气温,则下面四个函数模型中最合适的是( )
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 平均气温 | 21.4 | 26.0 | 36.0 | 48.8 | 59.1 | 68.6 |
| 月份 | 7 | 8 | 9 | 10 | 11 | 12 |
| 平均气温 | 73.1 | 71.9 | 64.7 | 53.5 | 39.8 | 27.7 |
A、y=26cos
| ||
B、y=26cos
| ||
C、y=-26cos
| ||
D、y=26sin
|
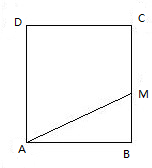 已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.
已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.