题目内容
△ABC中,角A,B,C所对边分别为a,b,c,已知a2+c2+
ac=b2,
(1)求B;
(2)设cosAcosC=
,
=
,求tanα.
| 2 |
(1)求B;
(2)设cosAcosC=
| 3 |
| 5 |
| 2 |
| cos(α+A)cos(α+C) |
| cos2α |
| ||
| 5 |
考点:余弦定理,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(1)由a2+c2+
ac=b2得a2+c2-b2=-
ac,根据余弦定理求出cosB的值,再求角B的值;
(2)根据两角和的余弦公式、商的关系、两角和的正弦公式化简
=
,再由内角和定理求出A+C=
,再求出sin(A+C)的值,根据条件、两角和余弦公式化简cos(A+C)求出sinAsinC的值,把数据代入化简后再求出tanα的值.
| 2 |
| 2 |
(2)根据两角和的余弦公式、商的关系、两角和的正弦公式化简
| cos(α+A)cos(α+C) |
| cos2α |
| ||
| 5 |
| π |
| 4 |
解答:
解:(1)由a2+c2+
ac=b2得,a2+c2-b2=-
ac,
由余弦定理得,cosB=
=-
,
∵0<B<π,∴B=
;
(2)由题意得,
=
,
则
=
,
(cosA-tanαsinA)(cosC-tanαsinC)=
化简得,cosAcosC-tanα(cosAsinC+tanαsinAcosC)+tan2αsinAsinC=
,
即cosAcosC-tanαsin(A+C)+tan2αsinAsinC=
,①
由B=
得,A+C=
,则sin(A+C)=
,
cos(A+C)=cosAcosC-sinAsinC=
,
把cosAcosC=
代入上式得,sinAsinC=
-
=
,
把上面的数据代入①得,
-
tanα+
tan2α=
,
化简得,tan2α-5tanα+4=0,
解得,tanα=1或tanα=4.
| 2 |
| 2 |
由余弦定理得,cosB=
| a2+c2-b2 |
| 2ac |
| ||
| 2 |
∵0<B<π,∴B=
| 3π |
| 4 |
(2)由题意得,
| cos(α+A)cos(α+C) |
| cos2α |
| ||
| 5 |
则
| (cosαcosA-sinαsinA)(cosαcosC-sinαsinC) |
| cos2α |
| ||
| 5 |
(cosA-tanαsinA)(cosC-tanαsinC)=
| ||
| 5 |
化简得,cosAcosC-tanα(cosAsinC+tanαsinAcosC)+tan2αsinAsinC=
| ||
| 5 |
即cosAcosC-tanαsin(A+C)+tan2αsinAsinC=
| ||
| 5 |
由B=
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
cos(A+C)=cosAcosC-sinAsinC=
| ||
| 2 |
把cosAcosC=
| 3 |
| 5 |
| 2 |
| 3 |
| 5 |
| 2 |
| ||
| 2 |
| ||
| 10 |
把上面的数据代入①得,
| 3 |
| 5 |
| 2 |
| ||
| 2 |
| ||
| 10 |
| ||
| 5 |
化简得,tan2α-5tanα+4=0,
解得,tanα=1或tanα=4.
点评:本题考查余弦定理,两角和的正弦、余弦公式,商的关系的综合应用,熟练掌握公式并会应用是解本题的关键,考查学生的化简计算能力.

练习册系列答案
相关题目
在一次文艺演出中,共有10上节目,其中舞蹈2个,歌曲3个,其它5个.若采用抽签的方式确定他们的演出顺序,则两个舞蹈排在一起,三个歌曲节目彼此分开的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
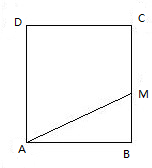 已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.
已知正方形ABCD的边长为2,有一动点M从点B出发沿正方形的边运动,路线是B→C→D→A,设点M经过的路程为x,△ABM的面积为S,求函数S=f(x)的解析式及其定义域.