题目内容
已知函数f(x)=sin(x+θ)+
cos(x+θ),θ∈[-
,
],且函数f(x)是偶函数,则θ的值为 .
| 3 |
| π |
| 2 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,函数奇偶性的性质,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值,三角函数的图像与性质
分析:首先对函数关系式进行恒等变换,把函数的关系式变形成正弦型函数,进一步利用函数的奇偶性求出结果.
解答:
解:f(x)=sin(x+θ)+
cos(x+θ)
=2(
sin(x+θ)+
cos(x+θ))
=2sin(x+θ+
)
当θ+
=kπ+
(k∈Z)
即:θ=kπ+
由于:θ∈[-
,
]
所以:当k=0时,θ=
故答案为:
| 3 |
=2(
| 1 |
| 2 |
| ||
| 2 |
=2sin(x+θ+
| π |
| 3 |
当θ+
| π |
| 3 |
| π |
| 2 |
即:θ=kπ+
| π |
| 6 |
由于:θ∈[-
| π |
| 2 |
| π |
| 2 |
所以:当k=0时,θ=
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,函数奇偶性的应用.属于基础题型.

练习册系列答案
相关题目
非零向量
,
满足
•
-2
2
2=0,|
|+|
|=1,则
与
的夹角的最小值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
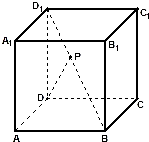 如图,点P在正方体ABCD-A1B1C1D1 的对角线BD1上,且cos∠PDA=
如图,点P在正方体ABCD-A1B1C1D1 的对角线BD1上,且cos∠PDA=
| ||
| 4 |
| A、75° | B、60° |
| C、45° | D、30° |
函数f(x)=cos
(
sin
+cos
)的在下列哪个区间上单调递增( )
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
A、(
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(-
|
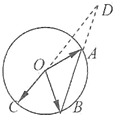 如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆外的点D,若
如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆外的点D,若| OC |
| OA |
| OB |
| A、(1,+∞) |
| B、(-∞,-1) |
| C、(0,1) |
| D、(-1,0) |
