题目内容
函数f(x)=cos
(
sin
+cos
)的在下列哪个区间上单调递增( )
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
A、(
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(-
|
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:由三角函数中的恒等变换应用化简函数解析式可得f(x)=sin(x+
)+
,由2kπ-
≤x+
≤2kπ+
,k∈Z可解得函数f(x)在[-
,
]区间上单调递增,结合选项即可得解.
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
解答:
解:∵f(x)=cos
(
sin
+cos
)
=
sinx+
=sin(x+
)+
,
∴由2kπ-
≤x+
≤2kπ+
,k∈Z可解得:2kπ-
≤x≤2kπ+
,k∈Z
∴当k=0时有函数f(x)在[-
,
]区间上单调递增,又(-
,0)?[-
,
].
故选:D.
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
=
| ||
| 2 |
| 1+cosx |
| 2 |
=sin(x+
| π |
| 6 |
| 1 |
| 2 |
∴由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 3 |
∴当k=0时有函数f(x)在[-
| 2π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
故选:D.
点评:三角函本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
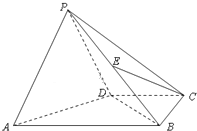 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=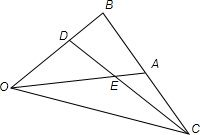 如图,已知△OAB中,点C是点B关于A的对称点,点D是线段OB的一个靠近B的三等分点,DC和OA交于E,设
如图,已知△OAB中,点C是点B关于A的对称点,点D是线段OB的一个靠近B的三等分点,DC和OA交于E,设