题目内容
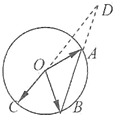 如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆外的点D,若
如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆外的点D,若| OC |
| OA |
| OB |
| A、(1,+∞) |
| B、(-∞,-1) |
| C、(0,1) |
| D、(-1,0) |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,由A,B,D三点共线,利用向量共线定理可得:存在实数λ满足
=λ
+(1-λ)
,又
=t
,t<-1,可得
=
+
,与
=m
+n
比较,即可得出.
| OD |
| OA |
| OB |
| OD |
| OC |
| OC |
| λ |
| t |
| OA |
| 1-λ |
| t |
| OB |
| OC |
| OA |
| OB |
解答:
解:如图所示,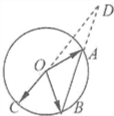
∵A,B,D三点共线,
∴存在实数λ满足
=λ
+(1-λ)
,
又
=t
,t<-1,
∴t
=λ
+(1-λ)
,
即
=
+
,与
=m
+n
比较,
可得m=
,n=
,
则m+n=
∈(-1,0).
∴m+n的取值范围是(-1,0).
故选:D.

∵A,B,D三点共线,
∴存在实数λ满足
| OD |
| OA |
| OB |
又
| OD |
| OC |
∴t
| OC |
| OA |
| OB |
即
| OC |
| λ |
| t |
| OA |
| 1-λ |
| t |
| OB |
| OC |
| OA |
| OB |
可得m=
| λ |
| t |
| 1-λ |
| t |
则m+n=
| 1 |
| t |
∴m+n的取值范围是(-1,0).
故选:D.
点评:本题考查了向量共线定理、平面向量基本定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知
与
为不共线的单位向量,其夹角θ,设
=λ
+
,
=
+μ
,有下列四个命题:
p1:|
+
|>|
-
|?θ∈(0,
);p2:|
+
|>|
-
|?θ∈(
,π);
p3:若A,B,C共线?λ+μ=1;p4:若A,B,C共线?λ•μ=1.其中真命题的是( )
| a |
| b |
| AB |
| a |
| b |
| AC |
| a |
| b |
p1:|
| a |
| b |
| a |
| b |
| π |
| 2 |
| a |
| b |
| a |
| b |
| π |
| 2 |
p3:若A,B,C共线?λ+μ=1;p4:若A,B,C共线?λ•μ=1.其中真命题的是( )
| A、p1,p4 |
| B、p1,p3 |
| C、p2,p3 |
| D、p2,p4 |
已知D为△ABC的边BC的中点,△ABC所在平面内有一个点P,满足
=
+
,则
的值为( )
| PA |
| PB |
| PC |
|
| ||
|
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
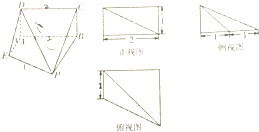 已知一个空间几何体的直观图和三视图(尺寸如图所示)
已知一个空间几何体的直观图和三视图(尺寸如图所示)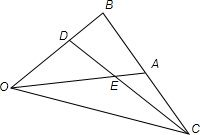 如图,已知△OAB中,点C是点B关于A的对称点,点D是线段OB的一个靠近B的三等分点,DC和OA交于E,设
如图,已知△OAB中,点C是点B关于A的对称点,点D是线段OB的一个靠近B的三等分点,DC和OA交于E,设