题目内容
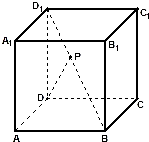 如图,点P在正方体ABCD-A1B1C1D1 的对角线BD1上,且cos∠PDA=
如图,点P在正方体ABCD-A1B1C1D1 的对角线BD1上,且cos∠PDA=
| ||
| 4 |
| A、75° | B、60° |
| C、45° | D、30° |
考点:异面直线及其所成的角
专题:空间角
分析:连结AP,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD-A1B1C1D1 的棱长为1,由cos∠PDA=
,求出P(3-
,3-
,
-2),由此能求出直线DP与CC1所成角的大小.
| ||
| 4 |
| 6 |
| 6 |
| 6 |
解答:
 解:连结AP,以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:连结AP,以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
设正方体ABCD-A1B1C1D1 的棱长为1,
则D1(0,0,1),B(1,1,0),D(0,0,0),
A(1,0,0),设P(a,b,c),
=λ
,0≤λ≤1,
∴(a,b,c-1)=(λ,λ,0),∴P(λ,λ,1-λ),
=(1,0,0),
=(λ,λ,1-λ),
∵cos∠PDA=
,
∴cos∠PDA=cos<
,
>
=
=
=
,
由0≤λ≤1,解得λ=3-
,
∴P(3-
,3-
,
-2),
=(3-
,3-
,
-2),
=(0,0,1),
设直线DP与CC1所成角为θ,
cosθ=|cos<
,
>|=
=
=
.
∴θ=60°,
∴直线DP与CC1所成角的大小为60°.
故选:B.
 解:连结AP,以D为原点,DA为x轴,DC为y轴,DD1为z轴,
解:连结AP,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1 的棱长为1,
则D1(0,0,1),B(1,1,0),D(0,0,0),
A(1,0,0),设P(a,b,c),
| D1P |
| D1B |
∴(a,b,c-1)=(λ,λ,0),∴P(λ,λ,1-λ),
| DA |
| DP |
∵cos∠PDA=
| ||
| 4 |
∴cos∠PDA=cos<
| DA |
| DP |
=
| ||||
|
|
| λ | ||
|
| ||
| 4 |
由0≤λ≤1,解得λ=3-
| 6 |
∴P(3-
| 6 |
| 6 |
| 6 |
| DP |
| 6 |
| 6 |
| 6 |
| CC1 |
设直线DP与CC1所成角为θ,
cosθ=|cos<
| DP |
| CC1 |
|
| ||||
|
|
| ||||
2
|
| 1 |
| 2 |
∴θ=60°,
∴直线DP与CC1所成角的大小为60°.
故选:B.
点评:本题考查两异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
“x>1”是“ln(ex+1)>1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、非充分非必要条件 |
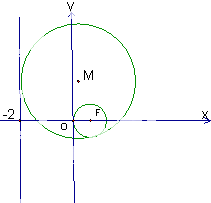 已知:动圆M与圆F:(x-1)2+y2=1内切,且与直线l:x=-2相切,动圆圆心 M的轨迹为曲线Γ
已知:动圆M与圆F:(x-1)2+y2=1内切,且与直线l:x=-2相切,动圆圆心 M的轨迹为曲线Γ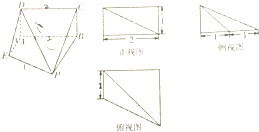 已知一个空间几何体的直观图和三视图(尺寸如图所示)
已知一个空间几何体的直观图和三视图(尺寸如图所示)