题目内容
如图,在四面体ABCD中,AB⊥面BCD,面ABC⊥面ACD,且∠ACB=∠CBD=45°,
(1)求证:BC⊥CD;
(2)求直线AC与平面ABD所成角的大小.

(1)求证:BC⊥CD;
(2)求直线AC与平面ABD所成角的大小.

考点:直线与平面所成的角,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得平面ABC⊥面BCD,面ABC⊥面ACD,从而CD⊥面ABC,由此能证明BC⊥CD.
(Ⅱ)由已知得面ABD⊥面BCD,BD是交线,过点C作CE⊥BD,则CE⊥平面ABD,连结AE,得∠CAE是直线与面ABD所成的角,由此能求出直线AC与平面ABD所成角.
(Ⅱ)由已知得面ABD⊥面BCD,BD是交线,过点C作CE⊥BD,则CE⊥平面ABD,连结AE,得∠CAE是直线与面ABD所成的角,由此能求出直线AC与平面ABD所成角.
解答:
(Ⅰ)证明:∵AB⊥平面BCD,AB?平面ABC,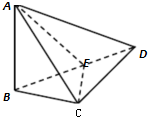
∴平面ABC⊥面BCD,又面ABC⊥面ACD,面BCD∩面ACD=CD,
∴CD⊥面ABC,∵CD?平面ABC,
∴BC⊥CD.
(Ⅱ)解:∵AB⊥平面BCD,AB?平面ABD,
∴面ABD⊥面BCD,BD是交线,
过点C作CE⊥BD,E是垂足,
则CE⊥平面ABD,连结AE,
得∠CAE是直线与面ABD所成的角,
由题意得BC是AC在面BCD上的射影,
由∠ACB=45°,得BC=
AC,
∵CE⊥BD,∠CBD=45°,∴CE=
BC=
AC,
在Rt△ACE中,sin∠CAE=
=
,∴∠CAE=30°,
∴直线AC与平面ABD所成角为30°.

∴平面ABC⊥面BCD,又面ABC⊥面ACD,面BCD∩面ACD=CD,
∴CD⊥面ABC,∵CD?平面ABC,
∴BC⊥CD.
(Ⅱ)解:∵AB⊥平面BCD,AB?平面ABD,
∴面ABD⊥面BCD,BD是交线,
过点C作CE⊥BD,E是垂足,
则CE⊥平面ABD,连结AE,
得∠CAE是直线与面ABD所成的角,
由题意得BC是AC在面BCD上的射影,
由∠ACB=45°,得BC=
| ||
| 2 |
∵CE⊥BD,∠CBD=45°,∴CE=
| ||
| 2 |
| 1 |
| 2 |
在Rt△ACE中,sin∠CAE=
| CE |
| AC |
| 1 |
| 2 |
∴直线AC与平面ABD所成角为30°.
点评:本题考查线面平行,线线垂直的性质的应用及证明,考查线面所成角的求法,解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用,是中档题.

练习册系列答案
相关题目
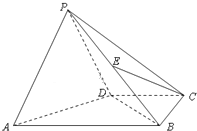 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=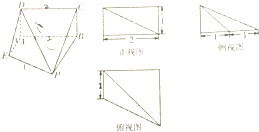 已知一个空间几何体的直观图和三视图(尺寸如图所示)
已知一个空间几何体的直观图和三视图(尺寸如图所示)