题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,直线
+
=1与圆x2+y2=
相切.
(1)求椭圆C的方程;
(2)设F2是椭圆C的右焦点,与坐标轴不平行的直线l经过F2与该椭圆交于A,B两点,P是A关于x轴的对称点,证明:直线BP与x轴的交点是个定点.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| x |
| a |
| y |
| b |
| 12 |
| 7 |
(1)求椭圆C的方程;
(2)设F2是椭圆C的右焦点,与坐标轴不平行的直线l经过F2与该椭圆交于A,B两点,P是A关于x轴的对称点,证明:直线BP与x轴的交点是个定点.
考点:直线与圆锥曲线的关系,椭圆的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)运用直线和圆相切的条件,即d=r,结合离心率公式及a,b,c的关系,解得a,b,进而得到椭圆方程;
(2)设出直线方程,联立椭圆方程,消去y,A(x1,y1),B(x2,y2),Q(m,0),P(x1,-y1),运用韦达定理,再由B,P,Q三点共线,运用斜率相等,整理转化为k,m的式子,即可得到m=4.
(2)设出直线方程,联立椭圆方程,消去y,A(x1,y1),B(x2,y2),Q(m,0),P(x1,-y1),运用韦达定理,再由B,P,Q三点共线,运用斜率相等,整理转化为k,m的式子,即可得到m=4.
解答:
(1)解:由于椭圆的离心率为
,则
=
,
即有a=2c,b=
c,
又直线
+
=1与圆x2+y2=
相切,
则d=
=
,即有
=
,
解得,c=1,则a=2,b=
.
则椭圆方程为:
+
=1;
(2)证明:设与坐标轴不平行经过F2的直线l的方程为y=k(x-1),
代入椭圆方程,消去y,得,(3+4k2)x2-8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),
即有x1+x2=
,x1x2=
,
由于P是A关于x轴的对称点,则P(x1,-y1),
设直线BP与x轴的交点为Q(m,0),
即有kBP=kBQ,
即为
=
,即有
=
,
化简可得,2x1x2=(m+1)(x1+x2)-2m,
即有
=(m+1)
-2m,
解得,m=4.
即有Q(4,0).
则直线BP与x轴的交点是个定点(4,0).
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
即有a=2c,b=
| 3 |
又直线
| x |
| a |
| y |
| b |
| 12 |
| 7 |
则d=
| |ab| | ||
|
2
| ||
| 7 |
2
| ||
|
2
| ||
| 7 |
解得,c=1,则a=2,b=
| 3 |
则椭圆方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)证明:设与坐标轴不平行经过F2的直线l的方程为y=k(x-1),
代入椭圆方程,消去y,得,(3+4k2)x2-8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),
即有x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
由于P是A关于x轴的对称点,则P(x1,-y1),
设直线BP与x轴的交点为Q(m,0),
即有kBP=kBQ,
即为
| y2+y1 |
| x2-x1 |
| y2 |
| x2-m |
| k(x1+x2-2) |
| x2-x1 |
| k(x2-1) |
| x2-m |
化简可得,2x1x2=(m+1)(x1+x2)-2m,
即有
| 2(4k2-12) |
| 3+4k2 |
| 8k2 |
| 3+4k2 |
解得,m=4.
即有Q(4,0).
则直线BP与x轴的交点是个定点(4,0).
点评:本题考查椭圆的方程和性质,考查直线和圆相切的条件,考查直线方程和椭圆方程联立,消去未知数,运用韦达定理,考查三点共线即为斜率相等,考查化简整理能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从数字1,2,3,…,10中,按由小到大的顺序取出a1、a2、a3,且a2-a1≥2,a3-a2≥2,则不同的取法有( )
| A、20种 | B、35种 |
| C、56种 | D、60种 |
设集合A={x||x-2|≤2},B={x|
>1},则∁R(A∩B)等于( )
| x |
| x+1 |
| A、{x|0≤x≤4} | B、R |
| C、{x|x<-1} | D、∅ |
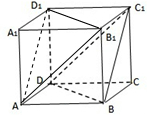 如图,正方体ABCD-A1B1C1D1.
如图,正方体ABCD-A1B1C1D1.