题目内容
已知抛物线y=4ax2(a>0)的准线与圆x2+y2+mx-
=0相切,且此抛物线上的点A(x0,2)到焦点的距离等于3,则m=( )
| 1 |
| 4 |
A、±
| ||
B、±
| ||
| C、1 | ||
| D、0 |
考点:圆与圆锥曲线的综合
专题:圆锥曲线的定义、性质与方程
分析:由抛物线方程求得其准线方程,再由圆与抛物线的准线相切得到
=
.由抛物线上的点A(x0,2)到焦点的距离等于3求得a的值,代入
=
求得m的值.
| m2+1 |
| 1 |
| 8a |
| m2+1 |
| 1 |
| 8a |
解答:
解:由抛物线y=4ax2(a>0),得x2=
y,
∴2p=
,
=
,
∴其准线方程为y=-
,
由x2+y2+mx-
=0,得(x+
)2+y2=
,
又抛物线y=4ax2(a>0)的准线与圆x2+y2+mx-
=0相切,
则
=
,
=
.
又抛物线上的点A(x0,2)到焦点的距离等于3,
则2+
=3,∴a=
.
∴
=2,解得m=±
.
故选:A.
| 1 |
| 4a |
∴2p=
| 1 |
| 4a |
| p |
| 2 |
| 1 |
| 16a |
∴其准线方程为y=-
| 1 |
| 16a |
由x2+y2+mx-
| 1 |
| 4 |
| m |
| 2 |
| m2+1 |
| 4 |
又抛物线y=4ax2(a>0)的准线与圆x2+y2+mx-
| 1 |
| 4 |
则
| 1 |
| 2 |
| m2+1 |
| 1 |
| 16a |
| m2+1 |
| 1 |
| 8a |
又抛物线上的点A(x0,2)到焦点的距离等于3,
则2+
| 1 |
| 16a |
| 1 |
| 16 |
∴
| m2+1 |
| 3 |
故选:A.
点评:本题考查了抛物线的简单几何性质,考查了抛物线的定义及圆的标准方程,考查了数学转化思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f(x)=lg(4-x2),则f(
)+f(
)的定义域是( )
| x |
| 2 |
| 2 |
| x |
| A、(-1,1) |
| B、(-4,4) |
| C、(-4,-1)∪(1,4) |
| D、(-2,-1)∪(1.2) |
已知向量
,
,
满足|
|=|
|+|
|,则( )
| AB |
| AC |
| BC |
| AB |
| AC |
| BC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
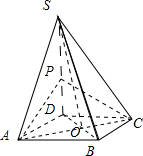 如图,四棱锥S-ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.
如图,四棱锥S-ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.