题目内容
已知向量
=(0,-1,1),
=(2,2,1),计算:
(1)|
|,|
|,|-3
|,|2
-
|;
(2)cos<
-
>;
(3)2
-
在-3
上的投影.
| a |
| b |
(1)|
| a |
| b |
| a |
| a |
| b |
(2)cos<
| a |
| b |
(3)2
| a |
| b |
| a |
考点:平面向量的综合题
专题:计算题,空间向量及应用
分析:(1)由模的坐标表示分别求|
|,|
|,|-3
|,|2
-
|;
(2)由数量积的定义数量积的坐标表示求cos<
-
>;
(3)由数量积的定义数量积的坐标表示求2
-
在-3
上的投影.
| a |
| b |
| a |
| a |
| b |
(2)由数量积的定义数量积的坐标表示求cos<
| a |
| b |
(3)由数量积的定义数量积的坐标表示求2
| a |
| b |
| a |
解答:
解:(1)|
|=
=
,
|
|=
=3,
|-3
|=3|
|=3
,
2
-
=(-2,-4,1);
故|2
-
|=
=
;
(2)cos<
-
>=
=
=-
;
(3)2
-
在-3
上的投影为
=
=-
.
| a |
| 02+(-1)2+12 |
| 2 |
|
| b |
| 22+22+12 |
|-3
| a |
| a |
| 2 |
2
| a |
| b |
故|2
| a |
| b |
| 22+42+12 |
| 21 |
(2)cos<
| a |
| b |
| ||||
|
|
| 0-2+1 | ||
|
| ||
| 6 |
(3)2
| a |
| b |
| a |
(2
| ||||||
|-3
|
| -3×4-1×3 | ||
3
|
5
| ||
| 2 |
点评:本题考查了空间向量的模的求法及空间向量数量积的定义应用,属于中档题.

练习册系列答案
相关题目
已知向量
,
,
满足|
|=|
|+|
|,则( )
| AB |
| AC |
| BC |
| AB |
| AC |
| BC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
下列说法不正确的是( )
| A、0∈N | ||
| B、-5∈Z | ||
| C、π∈Q | ||
D、-
|
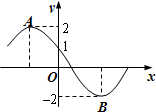 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,