题目内容
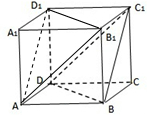 如图,正方体ABCD-A1B1C1D1.
如图,正方体ABCD-A1B1C1D1.(1)求证:AD1∥平面BDC1
(2)求证:平面AB1D1∥平面BDC1.
考点:平面与平面平行的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:已知几何体诶正方体,根据正方体的性质,利用线面平行的判定定理,面面平行的判定定理,证明线面平行和面面平行即可.
解答:
证明:(1)因为几何体是正方体,所以AB∥C1D1,AB=C1D1,
所以AD1∥BC1,
AD1?平面BDC1,BC1?平面BDC1,
所以AD1∥平面BDC1.
(2)在正方体中,根据正方体的性质可知BD∥B1D1,BC1∥AD1,
所以B1D1∥平面BDC1.
同理可证AD1∥平面BDC1.
又因为AD1∩D1B1=D1,
所以平面AB1D1∥平面BDC1.
所以AD1∥BC1,
AD1?平面BDC1,BC1?平面BDC1,
所以AD1∥平面BDC1.
(2)在正方体中,根据正方体的性质可知BD∥B1D1,BC1∥AD1,
所以B1D1∥平面BDC1.
同理可证AD1∥平面BDC1.
又因为AD1∩D1B1=D1,
所以平面AB1D1∥平面BDC1.
点评:本题主要考查了线面平行、面面平行的判定定理的应用,熟练掌握、运用相应的判定定理是关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
若a,b为实数,则“0<ab<1”是“a<
或b>
”的( )条件.
| 1 |
| b |
| 1 |
| a |
| A、充分必要 |
| B、充分而不必要 |
| C、必要而不充分 |
| D、既不充分也不必要 |
下列集合表示方法正确的是( )
| A、{1,3,3} |
| B、{全体实数} |
| C、{2,4} |
| D、不等式x2-1>2的解集是{x2-1>0} |
下列说法不正确的是( )
| A、0∈N | ||
| B、-5∈Z | ||
| C、π∈Q | ||
D、-
|
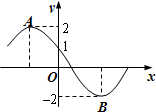 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,