题目内容
在△ABC中,BC=2
,D,E分别为边AC,AB上的中点,|BD|+|CE|=6,BD与CE交于点G,以直线BC为x轴,边BC的垂直平分线为y轴建立直角坐标系,记动点G形成的曲线为C
(1)求曲线C的方程;
(2)P,Q为曲线C上的两动点,且OP⊥OQ
①求证:点O到直线PQ的距离为定值;②求|PQ|min.
| 3 |
(1)求曲线C的方程;
(2)P,Q为曲线C上的两动点,且OP⊥OQ
①求证:点O到直线PQ的距离为定值;②求|PQ|min.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知得动点G的轨迹为以B,C为焦点的椭圆(去掉x轴上的两点),由此能求出曲线C的方程.
(2)①设P(x1,y1),Q(x2,y2),lOP:y=kx,则lOQ:y=-
x,联立
,得:xP2=
,同理可得xQ2=
,设点O到直线PQ的距离为h,由条件知OP•OQ=h•PQ,由此能证明h=
为定值.②PQ2=OP2+OQ2,由此利用均值定理能求出|PQ|min.
(2)①设P(x1,y1),Q(x2,y2),lOP:y=kx,则lOQ:y=-
| 1 |
| k |
|
| 4 |
| 1+4k2 |
| 4k2 |
| k2+4 |
2
| ||
| 5 |
解答:
(1)解:∵|GB|+|GC|=
|BD|+
|CE|=4>|BC|=2
,
∴动点G的轨迹为以B,C为焦点的椭圆(去掉x轴上的两点),
∴曲线C的方程为:
+y2=1(x≠0).
(2)①证明:由(1)知直线OP,OQ的斜率存在,
设P(x1,y1),Q(x2,y2),lOP:y=kx,
则lOQ:y=-
x,
联立方程组
,得:xP2=
,同理可得xQ2=
,
设点O到直线PQ的距离为h,由条件知OP•OQ=h•PQ,
∴OP2•OQ2=h2•PQ2,
又PQ2=OP2+OQ2,∴h2=
.
又OP2=xP2+yP2=
,
OQ2=xQ2+yQ2=
,∴
=
+
=
,
∴h=
为定值
②解:PQ2=OP2+OQ2=
≥
=
,
等号成立当且仅当k2=1,
∴|PQ|min=
.
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
∴动点G的轨迹为以B,C为焦点的椭圆(去掉x轴上的两点),
∴曲线C的方程为:
| x2 |
| 4 |
(2)①证明:由(1)知直线OP,OQ的斜率存在,
设P(x1,y1),Q(x2,y2),lOP:y=kx,
则lOQ:y=-
| 1 |
| k |
联立方程组
|
| 4 |
| 1+4k2 |
| 4k2 |
| k2+4 |
设点O到直线PQ的距离为h,由条件知OP•OQ=h•PQ,
∴OP2•OQ2=h2•PQ2,
又PQ2=OP2+OQ2,∴h2=
| OP2•OQ2 |
| OP2+OQ2 |
又OP2=xP2+yP2=
| 4(1+k2) |
| 1+4k2 |
OQ2=xQ2+yQ2=
| 4(1+k2) |
| k2+4 |
| 1 |
| h2 |
| 1 |
| OP2 |
| 1 |
| OQ2 |
| 5 |
| 4 |
∴h=
2
| ||
| 5 |
②解:PQ2=OP2+OQ2=
| 20(1+k2)2 |
| (k2+4)(1+4k2) |
| 20(1+k2) | ||
[
|
| 16 |
| 5 |
等号成立当且仅当k2=1,
∴|PQ|min=
4
| ||
| 5 |
点评:本题考查曲线方程的求法,考查点到直线的距离为定值的证明,考查线段长的最小值的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
已知点P(x,y)的坐标满足条件
,则x2+y2的最大值为( )
|
| A、17 | B、18 | C、20 | D、21 |
若a,b为实数,则“0<ab<1”是“a<
或b>
”的( )条件.
| 1 |
| b |
| 1 |
| a |
| A、充分必要 |
| B、充分而不必要 |
| C、必要而不充分 |
| D、既不充分也不必要 |
已知集合A={x|y=lg(1-x)},集合B={y|y=x+
,x≠0},则A∩B=( )
| 1 |
| x |
| A、空集∅ |
| B、{x|x<1且x≠0} |
| C、(-∞,-2] |
| D、(-∞,1) |
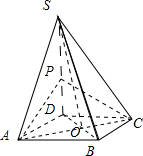 如图,四棱锥S-ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.
如图,四棱锥S-ABCD中,底面ABCD是菱形,其对角线的交点为O,且SA=SC,SA⊥BD.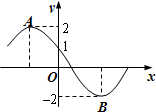 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,