题目内容
定义域为R的奇函数f（x）单调递增，且对任意实数a，b满足f（a）+f（b-1）=0，则a+b=（ ）
| A、-1 | B、0 | C、1 | D、不确定 |
考点：奇偶性与单调性的综合,函数奇偶性的性质
专题：计算题,函数的性质及应用
分析：由函数的奇偶性及f（a）+f（b-1）=0，可得f（b-1）=-f（a）=f（-a），再由单调性可去掉符号“f”．
解答：
解：∵f（x）为R上的奇函数，
∴f（a）+f（b-1）=0，可化为f（b-1）=-f（a）=f（-a），
又f（x）在R上单调递增，
∴b-1=-a，即a+b=1，
故选C．
∴f（a）+f（b-1）=0，可化为f（b-1）=-f（a）=f（-a），
又f（x）在R上单调递增，
∴b-1=-a，即a+b=1，
故选C．
点评：该题考查函数的单调性奇偶性的综合应用，属基础题，正确理解函数的有关性质是解题关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
已知函数y=f（x）的图象如图所示，则下列说法中错误的是（ ）
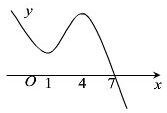
| A、f（x）在区间（-∞，1）上单调递减 |
| B、f（x）在区间（1，4）上单调递增 |
| C、当4＜x＜7时，f'（x）＞0 |
| D、当x=1时，f'（x）=0 |
设集合A={x|x＞-1}，B={x|x≥1}，则“x∈A且x∉B”成立的充要条件是（ ）
| A、-1＜x≤1 | B、x≤1 |
| C、x＞-1 | D、-1＜x＜1 |
已知x的不等式a（x-a）（x-
）＞0，其中0＜a＜1，则它的解是（ ）
| 1 |
| a |
A、{x|x＜a或x＞
| ||
| B、{x|x＞a} | ||
C、{x|x＜
| ||
D、{x|x＜
|
函数y=
的导数是（ ）
| 1 |
| x |
| A、y'=ex | ||
| B、y'=lnx | ||
C、y′=
| ||
| D、y'=-x-2 |
若集合A={x||x|≤1，x∈R}，集合B为函数f（x）=log2（3x+1）的值域，则A∩B=（ ）
| A、{x|0＜x≤1} |
| B、{x|x≥0} |
| C、{x|0≤x≤1} |
| D、∅ |
下列函数中，值域是（0，+∞）的函数是（ ）
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=（
|
y=2x+1在[1，2]内的平均变化率为（ ）
| A、3 | B、2 | C、1 | D、0 |
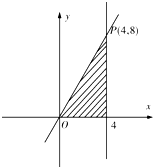设不等式组