题目内容
 设不等式组
设不等式组
|
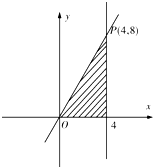
(1)n=2时,先在平面直角坐标系中作出区域D2,再求a2的值;
(2)求数列{an}的通项公式;
(3)记数列{an}的前n项的和为Sn,试证明:对任意n∈N*恒有
| S1 |
| 22S2 |
| S2 |
| 32S3 |
| Sn |
| (n+1)2Sn+1 |
| 5 |
| 12 |
考点:数列与不等式的综合
专题:综合题,等差数列与等比数列
分析:(1)在4×8的矩形区域内有5×9个整点,对角线上有5个整点,可求a2的值;
(2)直线y=nx与x=4交于点P(4,4n),即可求数列{an}的通项公式;
(3)利用裂项法,放缩,求和即可证明结论.
(2)直线y=nx与x=4交于点P(4,4n),即可求数列{an}的通项公式;
(3)利用裂项法,放缩,求和即可证明结论.
解答:
解:(1)D2如图中阴影部分所示,
∵在4×8的矩形区域内有5×9个整点,对角线上有5个整点,
∴a2=
=25.(3分)
(另解:a2=1+3+5+7+9=25)
(2)直线y=nx与x=4交于点P(4,4n),
据题意有an=
=10n+5.(6分)
(另解:an=1+(n+1)+(2n+1)+(3n+1)+(4n+1)=10n+5)
(3)Sn=5n(n+2). (8分)
∵
=
=
•
<
,
∴
+
+…+
<
+
+…+
=
(
-
+…+
-
)=
(
+
-
-
)<
(13分)
∵在4×8的矩形区域内有5×9个整点,对角线上有5个整点,
∴a2=
| 5×9+5 |
| 2 |
(另解:a2=1+3+5+7+9=25)
(2)直线y=nx与x=4交于点P(4,4n),
据题意有an=
| 5×(4n+1)+5 |
| 2 |
(另解:an=1+(n+1)+(2n+1)+(3n+1)+(4n+1)=10n+5)
(3)Sn=5n(n+2). (8分)
∵
| Sn |
| (n+1)2Sn+1 |
| n(n+2) |
| (n+1)2(n+1)(n+3) |
| 1 |
| (n+1)(n+3) |
| n(n+2) |
| (n+1)2 |
| 1 |
| (n+1)(n+3) |
∴
| S1 |
| 22S2 |
| S2 |
| 32S3 |
| Sn |
| (n+1)2Sn+1 |
| 1 |
| 2×4 |
| 1 |
| 3×5 |
| 1 |
| (n+1)(n+3) |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+2 |
| 1 |
| n+3 |
| 5 |
| 12 |
点评:本题考查数列与不等式的综合,考查数列的通项与求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
定义域为R的奇函数f(x)单调递增,且对任意实数a,b满足f(a)+f(b-1)=0,则a+b=( )
| A、-1 | B、0 | C、1 | D、不确定 |
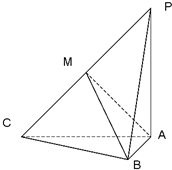 如图,三棱锥P-ABC中,
如图,三棱锥P-ABC中,