题目内容
证明sin(α+β)sin(α-β)=sin2α-sin2β,并利用该式计算sin220°+sin80°•sin40°的值.
考点:三角函数恒等式的证明
专题:三角函数的求值
分析:根据两角和的正弦公式乘以两角差的正弦公式,再根据1=sin2α+cos2α,化简即可证明,sin80°•sin40°=sin(60°+20°)•sin(60°-20°),问题得以解决.
解答:
证明:∵sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ,
∴sin(α+β)sin(α-β)=sin2αcos2β-cos2αsin2β=sin2α(1-sin2β)-(1-sin2α)sin2β=sin2α-sin2αsin2β-sin2β+sin2αsin2β=sin2α-sin2β,
∴sin(α+β)sin(α-β)=sin2α-sin2β;
∴sin220°+sin80°•sin40°=sin220°+sin(60°+20°)•sin(60°-20°)=sin220°+sin260°-sin220°=sin260°=
∴sin(α+β)sin(α-β)=sin2αcos2β-cos2αsin2β=sin2α(1-sin2β)-(1-sin2α)sin2β=sin2α-sin2αsin2β-sin2β+sin2αsin2β=sin2α-sin2β,
∴sin(α+β)sin(α-β)=sin2α-sin2β;
∴sin220°+sin80°•sin40°=sin220°+sin(60°+20°)•sin(60°-20°)=sin220°+sin260°-sin220°=sin260°=
| 3 |
| 4 |
点评:本题主要考查三角函数的和差公式以及平方关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数y=sin(2x+φ)在(
,
)上单调递增,其中φ∈(π,2π),则φ的取值范围为( )
| π |
| 4 |
| π |
| 3 |
A、[
| ||||
B、(π,
| ||||
C、[
| ||||
D、[
|
函数f(x)=lg(|x|+1)-sin2x的零点个数为( )
| A、9 | B、10 | C、11 | D、12 |
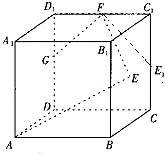 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,DD1的中点.设点E1是点E在平面DCC1D1内的正投影.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,DD1的中点.设点E1是点E在平面DCC1D1内的正投影.