题目内容
在三角形ABC中，a，b，c分别是角A，B，C的对边，2a=b+c，且sin2A=sinBcosC，判断三角形形状．
考点：三角形的形状判断,正弦定理
专题：解三角形
分析：由sin2A=sinBcosC结合正弦定理可得a2=bc，又2a=b+c，由联立可解得b=c，从而可判断△ABC为等腰三角形．
解答：
解：∵sin2A=sinBcosC，结合正弦定理可得：a2=bc，①
又∵2a=b+c，②
∴由①②联立可解得：
=bc，
∴解得：（b-c）2=0，
∴可得：b=c．
即有△ABC为等腰三角形．
又∵2a=b+c，②
∴由①②联立可解得：
| (a+c)2 |
| 4 |
∴解得：（b-c）2=0，
∴可得：b=c．
即有△ABC为等腰三角形．
点评：本题主要考察了正弦定理在解三角形中的应用，属于基本知识的考查．
练习册系列答案
相关题目
在平行四边形ABCD中，对角线AC与BD交于点O，若
+
=λ
，则实数λ等于（ ）
| AB |
| AD |
| AO |
| A、4 | B、3 | C、2 | D、1 |
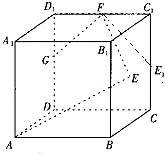如图，已知正方体ABCD-A1B1C1D1的棱长为2，点E是正方形BCC1B1的中心，点F，G分别是棱C1D1，DD1的中点．设点E1是点E在平面DCC1D1内的正投影．
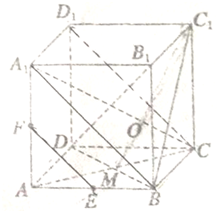如图，在正方体ABCD-A1B1C1D1，对角线A1C与平面BDC1交于点O．AC、BD交于点M、E为AB的中点，F为AA1的中点，