如图.AB.CD是⊙O的两条直径.P是圆周上任一点.作PM⊥AB.PN⊥CD.AH⊥CD.求证:MN=AH．题目和参考答案——青夏教育精英家教网—

题目内容

16．

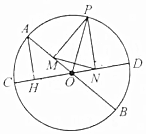如图，AB、CD是⊙O的两条直径，P是圆周上任一点，作PM⊥AB，PN⊥CD，AH⊥CD，求证：MN=AH．

分析运用四点共圆和正弦函数定义，结合诱导公式，即可证明结论．

解答证明：由题意，P，M，O，N四点共圆，∴$\frac{MN}{sin∠MPN}$=OP，
∴MN=OPsin∠MPN=OPsin∠MON，
∵AH=OAsin∠AOH，∠AOH+∠MON=180°，
∴MN=AH．

点评本题考查四点共圆和正弦函数定义，考查学生分析解决问题的能力，属于中档题．

练习册系列答案

相关题目

4．记a=sin1，b=sin2，c=sin3，则（　　）

5．若函数$f（x）=\frac{1}{3}{x^3}-{x^2}-3x-a$有三个不同的零点，则实数a的取值范围是$（-9，\frac{5}{3}）$．

4．

“健步走”是一种方便而又有效的锻炼方式，李老师每天坚持“健步走”，并用计步器进行统计．他最近8天“健步走”步数的条形统计图及相应的消耗能量数据表如表：

步数（千卡）	16	17	18	19
消耗能量（卡路里）	400	440	480	520

（1）求李老师这8天“健步走”步数的平均数；
（2）从步数为16千步，17千步，18千步的6天中任选2天，设李老师这2天通过“健步走”消耗的能量和为X，求X的分布列及数学期望．

11．已知函数f（x）=sin2xcos2φ+cos2xsin2φ（φ＞0）的图象关于直线x=$\frac{π}{3}$对称，则φ 的最小值为$\frac{5π}{12}$．

1．

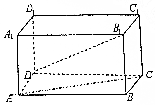如图，在长方体ABCD-A₁B₁C₁D₁中，AD=AA₁=1，AB=2．
（I）求异面直线AC与B₁D所成角的余弦值；
（Ⅱ）设M是线段B₁D上一点，在长方体ABCD-A₁B₁C₁D₁内随机选取一点，若该点取自于三棱锥M-ACD内的概率为$\frac{1}{18}$，试确定点M的位置．

8．已知f（x）=ax⁷-bx⁵+cx³+2，且f（-5）=m，则f（5）的值为（　　）

5．已知A={x|2^x＞1}，B={x|log₃（x+1）＜1}．
（1）求A∪B及（∁_RA）∩B；
（2）若集合C={x|x＜a}，满足B∪C=C，求实数a的取值范围．

6．若直角坐标平面内两点A，B满足：
①A，B均在函数f（x）的图象上；
②A，B关于原点对称．
则称点对[A，B]为函数f（x）的一对“匹配点对”（点对[A，B]与[B，A]视作同一对）．
若函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x，x＞0}\\{-{x}^{2}-4x，x≤0}\end{array}\right.$，则此函数的“匹配点对”共有（　　）对．

试题分类