题目内容
6.若直角坐标平面内两点A,B满足:①A,B均在函数f(x)的图象上;
②A,B关于原点对称.
则称点对[A,B]为函数f(x)的一对“匹配点对”(点对[A,B]与[B,A]视作同一对).
若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}x,x>0}\\{-{x}^{2}-4x,x≤0}\end{array}\right.$,则此函数的“匹配点对”共有( )对.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 首先弄清关于原点对称的点的特点,进而把问题转化为只需考查y=${log}_{\frac{1}{2}}^{x}$与y=x2-4x (x>0)的交点个数即可,
解答  解:函数y=-x2-4x (x<0)关于原点对称的图象解析式为y=x2-4x (x>0),只需考查y=${log}_{\frac{1}{2}}^{x}$与y=x2-4x (x>0)的交点个数即可,
解:函数y=-x2-4x (x<0)关于原点对称的图象解析式为y=x2-4x (x>0),只需考查y=${log}_{\frac{1}{2}}^{x}$与y=x2-4x (x>0)的交点个数即可,
在同一直角坐标系中画出两图象,如图所示,可得匹配点对”共有1对.
故选:B.
点评 本题考查了函数的零点,利用对称性转化为初等函数的交点是关键,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
17.若α,β∈(0,π)且 $tanα=\frac{1}{2},tanβ=\frac{1}{3}$,则α+β=( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
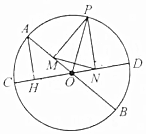 如图,AB、CD是⊙O的两条直径,P是圆周上任一点,作PM⊥AB,PN⊥CD,AH⊥CD,求证:MN=AH.
如图,AB、CD是⊙O的两条直径,P是圆周上任一点,作PM⊥AB,PN⊥CD,AH⊥CD,求证:MN=AH.