题目内容
11.已知函数f(x)=sin2xcos2φ+cos2xsin2φ(φ>0)的图象关于直线x=$\frac{π}{3}$对称,则φ 的最小值为$\frac{5π}{12}$.分析 f(x)=sin2xcos2φ+cos2xsin2φ=sin(2x+2φ)的图象关于直线x=$\frac{π}{3}$对称,可得2×$\frac{π}{3}$+2φ=kπ+$\frac{π}{2}$,即可求出φ 的最小值.
解答 解:∵f(x)=sin2xcos2φ+cos2xsin2φ=sin(2x+2φ)的图象关于直线x=$\frac{π}{3}$对称,
∴2×$\frac{π}{3}$+2φ=kπ+$\frac{π}{2}$,
∴φ=$\frac{kπ}{2}$-$\frac{π}{12}$,
∵φ>0,∴φ 的最小值为$\frac{5π}{12}$,
故答案为$\frac{5π}{12}$.
点评 本题考查和角的正弦公式,考查三角函数图象的对称性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.函数f(x)=log3x+x-3的零点所在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
6.函数$f(x)=\frac{1}{{ln({3x+1})}}$的定义域是( )
| A. | $({-\frac{1}{3},+∞})$ | B. | $({-\frac{1}{3},0})∪({0,+∞})$ | C. | $[{-\frac{1}{3},+∞})$ | D. | [0,+∞) |
3.下列函数中,同时满足两个条件“①?x∈R,f($\frac{π}{12}+x$)+f($\frac{π}{12}-x$)=0;②当-$\frac{π}{6}$<x<$\frac{π}{3}$时,f′(x)>0”的一个函数是( )
| A. | f(x)=sin(2x+$\frac{π}{6}$) | B. | f(x)=cos(2x+$\frac{π}{3}$) | C. | f(x)=sin(2x-$\frac{π}{6}$) | D. | f(x)=cos(2x-$\frac{π}{6}$) |
20.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
| A. | y=x+1 | B. | y=-x2+1 | C. | y=|x|+1 | D. | $y=1-\frac{1}{x}$ |
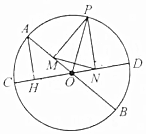 如图,AB、CD是⊙O的两条直径,P是圆周上任一点,作PM⊥AB,PN⊥CD,AH⊥CD,求证:MN=AH.
如图,AB、CD是⊙O的两条直径,P是圆周上任一点,作PM⊥AB,PN⊥CD,AH⊥CD,求证:MN=AH.