题目内容
5.已知A={x|2x>1},B={x|log3(x+1)<1}.(1)求A∪B及(∁RA)∩B;
(2)若集合C={x|x<a},满足B∪C=C,求实数a的取值范围.
分析 (1)化简集合A、B,根据定义写出A∪B、CRA和(CRA)∩B;
(2)根据B∪C=C得出B⊆C,由此求出a的取值范围.
解答 解:(1)集合A={x|2x>1}={x|x>0},
B={x|log3(x+1)<1}={x|0<x+1<3}={x|-1<x<2};…(2分)
∴A∪B={x|x>-1},
CRA={x|x≤0};…(5分)
∴(CRA)∩B={x|-1<x≤0};…(7分)
(2)∵B={x|-1<x<2},C={x|x<a},
∵B∪C=C,
∴B⊆C,…(9分)
∴a≥2;
即a的取值范围是a≥2.…(12分)
点评 本题考查了集合的定义与计算问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若复数z满足,(4+3i)z=|3-4i|,则z的虚部为( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | -$\frac{3}{5}$i | D. | -$\frac{4}{5}$i |
20.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是( )
| A. | y=x+1 | B. | y=-x2+1 | C. | y=|x|+1 | D. | $y=1-\frac{1}{x}$ |
10.若存在非零的实数a,使得f(x)=f(a-x)对定义域上任意的x恒成立,则函数f(x)可能是( )
| A. | f(x)=x2-2x+1 | B. | f(x)=x2-1 | C. | f(x)=2x | D. | f(x)=2x+1 |
17.若α,β∈(0,π)且 $tanα=\frac{1}{2},tanβ=\frac{1}{3}$,则α+β=( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{7π}{4}$ |
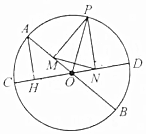 如图,AB、CD是⊙O的两条直径,P是圆周上任一点,作PM⊥AB,PN⊥CD,AH⊥CD,求证:MN=AH.
如图,AB、CD是⊙O的两条直径,P是圆周上任一点,作PM⊥AB,PN⊥CD,AH⊥CD,求证:MN=AH.