题目内容
给出如下四个判断:
①?x0∈R,ex0≤0;
②?x∈R+,2x>x2;
③设集合A={x|
<0},B={x|x-1|<a},则“a=1”是“A∩B≠∅”的必要不充分条件;
④
,
为单位向量,其夹角为θ,若|
-
|>1,则
<θ≤π.
其中正确的判断个数是( )
①?x0∈R,ex0≤0;
②?x∈R+,2x>x2;
③设集合A={x|
| x-1 |
| x+1 |
④
| a |
| b |
| a |
| b |
| π |
| 3 |
其中正确的判断个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:①②列举反例;③利用必要不充分条件的定义,进行验证;根据向量的数量积公式,可得结论.
解答:
解:①?x∈R,ex>0,故不正确;
②x=2或4时,2x=x2,故不正确;
③集合A={x|
<0}=(-1,1),a=1时,B={x|x-1|<a}=(0,2),A∩B≠∅,反过来,“A∩B≠∅”时,不一定有a=1,故不正确;
④
,
为单位向量,其夹角为θ,若|
-
|>1,则cosθ<
,∵θ∈[0,π],∴
<θ≤π,故正确.
故选:A.
②x=2或4时,2x=x2,故不正确;
③集合A={x|
| x-1 |
| x+1 |
④
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| π |
| 3 |
故选:A.
点评:本题考查命题的真假判断与应用,考查学生分析解决问题的能力,假命题列举反例即可.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
若实数a,b,c满足a2+b2+c2=8,则a+b+c的最大值为( )
| A、9 | ||
B、2
| ||
C、3
| ||
D、2
|
设y=sin2x,则y′=( )
| A、sin2x |
| B、2sinx |
| C、cos2x |
| D、cos2x |
给出下列四个命题,其中假命题是( )
| A、从匀速传递的新产品生产流水线上,质检员每10分钟从中抽取一件新产品进行某项指标检测,这样的抽样是分层抽样 | ||
| B、样本方差反映了样本数据与样本平均值的偏离程度 | ||
| C、在回归分析模型中,残差平方和越小,说明模型的拟合效果越好 | ||
D、设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(-1<x<0)=
|
 如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则这三个数位于不同行不同列的概率是
如图,三行三列的方阵中有9个数aij(i=1,2,3;j=1,2,3),从中任取三个数,则这三个数位于不同行不同列的概率是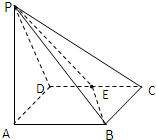 如图,四棱锥P-ABCD中,ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成角60°
如图,四棱锥P-ABCD中,ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成角60°